Нарисуй не отрывая руки. Как и почему?
Наверно всем знакома эта игра, и в особенности центральная фигура. Кто-то ее называет "открытый конверт", кто-то "домик". И большинство (если не все) могут его нарисовать не отрывая руки, и даже не одним способом. Кто-то наверняка пробовал и закрытый конверт нарисовать, но как ни старался, по правилам его не удавалось нарисовать. Я один из них. Мне стало интересно, в чем же секрет. И я нашел ответ, а вместе с этим пару секретов и любопытных моментов.
Кому-то материал покажется очевидным, а для кого-то, может, покажется интересным, и одним вопросом станет меньше.
"Домик" или "Открытый конверт"
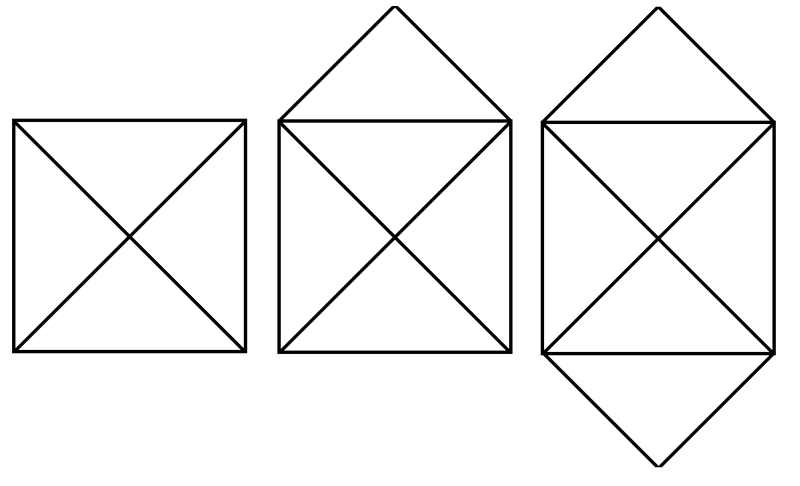
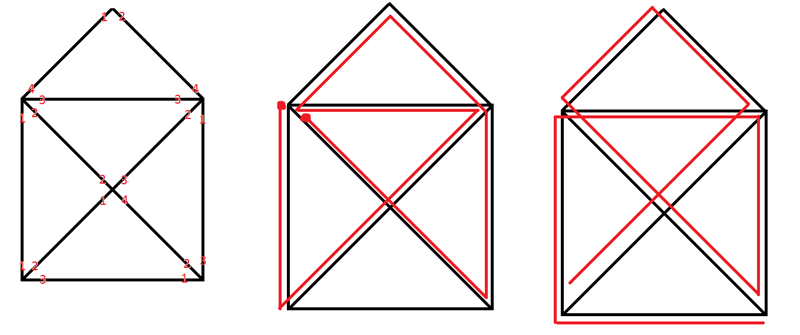
Рассмотрим самую распространенную фигуру "домик" или "открытый конверт". Когда-то я искал самые разные вариант решения этой задачки, но заметил, что успешные только те, которые начинаются с нижних углов. К тому же в этом случае любое движение было правильным (рисунок справа). Но стоит взять любую другую точку всегда остается хотя бы одна линия (рисунок посередине). Изучив в чем же особенность этих углов, я заметил, что нижние углы являются пересечением нечетного количества линий (далее "нечетная точка") (рисунок слева). И при этом начало лежит в одном, а конец всегда в другом углу.
Давайте перейдем к другой таинственной фигуре.
"Закрытый конверт"
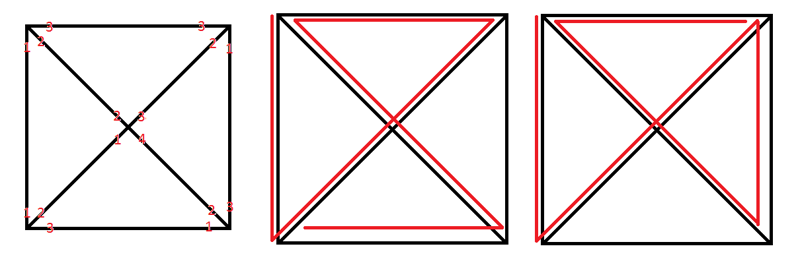
Из ранее обнаруженного можно сделать вывод, что в данном случае можно начать с любого угла, т.к. они все нечетные точки. Но как ни старайся остается хотя бы одна линия. Так в чем же проблема? Может их слишком много? А что будет, если нечетных точек не будет вовсе?
"Развернутый конверт"
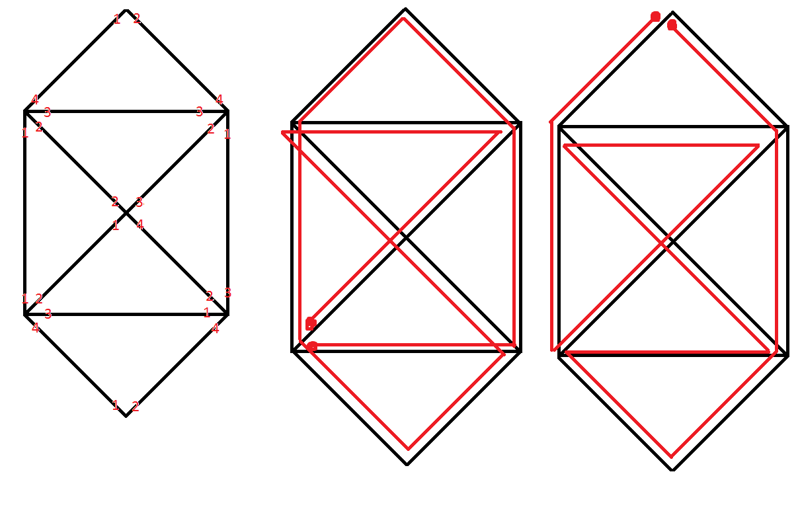
В данном случае я выяснил, что можно начинать откуда угодно. При этом начало и конец всегда в одной точке.
В результате я понял, что чтобы было решение - нечетных точек должно быть либо только 2, либо ни одной. Но почему?
Дело в том, что если в точке пересекается четное количество линий, значит ручка будет заходить и выходить в нее одинаковое количество раз. А если в пересечении - нечетное количество, значит входить или выходить из него ручка будет на один раз больше. И соответственно одна линия не может начинаться и заканчиваться несколько раз. Поэтому:
1) В "Закрытом конверте" 4 нечетные точки, и линия должна 2 раза начинаться и 2 раза заканчиваться. И поэтому невозможно по правилам нарисовать.
2) В "Открытом конверте" 2 нечетные точки, значит в одной нечетной точке она должна начинаться, а в другой - заканчиваться.
3) В "Раскрытом конверте" нечетных точек - нет, значит линия начинаться может в любой точке, но чтобы она была "четной", в ней линия должна и закончиться.
Подведем итог.
1) Чтобы сразу понять можно ли нарисовать фигуру по правилам, посчитайте, сколько в ней нечетных точек (точек с пересечение нечетного количества линий). Если больше 2, то нарисовать - невозможно.
2) Если в фигуре 2 нечетные точки, то начинать нужно с любой из них. Линия в результате всегда придет во вторую нечетную точку.
3) Если в фигуре нет нечетных точек, то начать можно откуда угодно, даже не с пересечения, и в результате линия всегда будет приходить в начальную точку.
P.S. Простите, если что-то не так в моем посте, он у меня первый. Уж очень захотелось поделиться наблюдениями. Спасибо за внимание!


14 комментариев
7 лет назад
Рисуем ;)
Удалить комментарий?
Удалить Отмена7 лет назад
Удалить комментарий?
Удалить Отмена7 лет назад
Удалить комментарий?
Удалить Отмена7 лет назад
Удалить комментарий?
Удалить Отмена7 лет назад
>> но заметил, что успешные только те, которые начинаются с нижних углов
Домик этот рисуется с любой точки и как угодно ! Всё дело в крыше...
Удалить комментарий?
Удалить Отмена7 лет назад
Удалить комментарий?
Удалить Отмена7 лет назад
Удалить комментарий?
Удалить Отмена7 лет назад
Впрочем, ты сможешь меня легко посрамить продемонстрировав такой, известный только тебе, способ. Тем самым ты посрамишь не только меня и автора статьи, но заодно и опровергнешь математическое обоснование теории графов.
Удалить комментарий?
Удалить Отмена7 лет назад
Удалить комментарий?
Удалить Отмена