Пи это не константа
Речь пойдет о такой штуке как окружность и связанной с ней базовой константой Пи, без которых нет ни синусов ни косинусов, нет ни электроники ни всего того от чего зависит наша жизнь.
Я пойду по стопам древних и буду вычислять пи тем же методом что и пользовался Архимед и последователи, но цель не найти формулу которая вычислит пи до последнего знака (это невозможно - пи не вычислимо) а показать на простом примере те грабли на которые наступили древние и по которым ходим мы. По моим давним наблюдениям, "грабли" возникают от того, что мы в качестве инструмента для познания чего либо используем то что есть под руками, а оно не всегда для того хорошо подходит. Итак, главные виновники торжества: смотрим на руки, на две свои руки и пять пальцев на каждой. 2*5=10, говорим им спасибо, так как именно им мы обязаны своей привычной десятичной системе исчисления. Далее календарь - 365 дней в году. Древние ошибочно полагали, что в году 360 дней, отсюда пошло наше привычное деление окружности на 360 градусов. 360 если разложить на множители это будет 2*3*2*3*2*5, так как с десятичной системой сие согласуется не очень (есть множители отличные от 2 и 5), то были умники которые придумали грады, когда прямой угол равен 100% (это до сих пор используется у топологов и можно видеть на дорожных знаках предупреждающих об опасном спуске/подъеме) при этом вся окружность 400 град или 2*2*2*5*2*5, уже как бы привычнее но отчего-то не прижилось. А универсальными радианами пользуются математики, но радиана нет без Пи, а само Пи не вычислимо... Далее дополним список простейшим - лист бумаги, линейку и циркуль, на листе чертим прямую и окружность. Внимательно смотрим на то, что получилось. Итак, что мы нарисовали? Прямую? Окружность? Смотрим внимательно. Не разглядели? Ну тогда берем стопку черновиков или какой не сильно нужной бумаги, карандаш, и лезем в теорию по стопам древних...
Я начну с того, что буду искать Пи методом приближения последовательно вписывая в окружность различные правильные многоугольники. Начну с квадрата как и Архимед, и потом буду удваивать число сторон. Без чертежей суть понять очень трудно, а самому их рисовать лень, поэтому я буду приводить что удалось гуглем найти да стырить посему сорри за качество. Архимед последовательно вписывал и описывал многоугольники, я буду действовать так же:
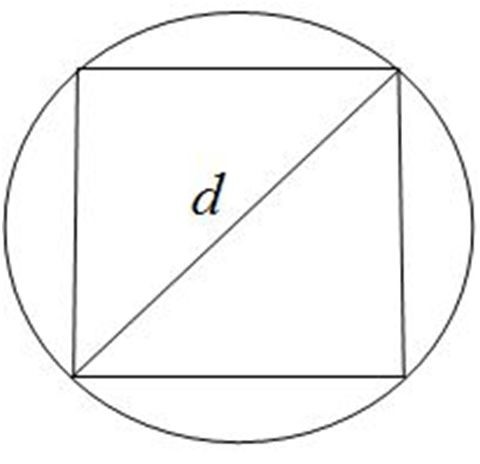
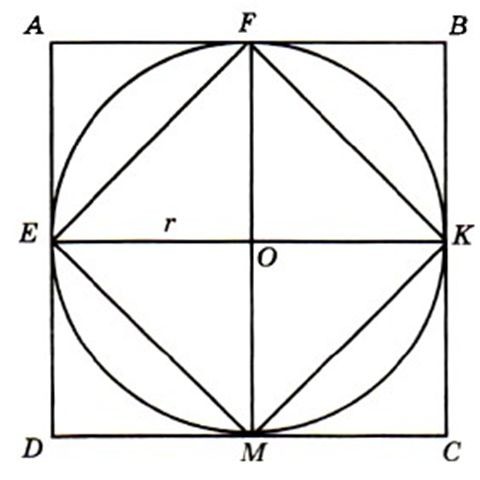
Периметр вписанного многоугольника всегда меньше длины окружности а описанного всегда больше - очевидно из чертежа, так как кривая окружности проходит через два угла треугольника AEF не совпадая при этом с основанием EF и не выходя за вершину А, а так как сумма двух сторон треугольника всегда больше третьей то внешний многоугольник всегда будет больше а внутренний всегда меньше и мы имеем как бы "коридор" в который зажата искомая пи, она всегда будет больше чем периметр внутреннего многоугольника и всегда меньше внешнего, далее попробуем эти периметры найти для квадрата. Для удобства диаметр окружности принят равным 1 (потому как Пи это отношение к диаметру окружности а не к радиусу) тогда диагонали квадрата EFKM равны 1 и стороны квадрата ABCD тоже равны 1. Вспоминаем теорему Пифагора и находим сторону квадрата EFKM. Принимаем ее за х, тогда
х^2+x^2=1
2*x^2=1
x^2 =1/2
x=sqrt(1/2)=1/sqrt(2)=sqrt(2)/2 (sqrt() - функция извлечения корня квадратного)
тогда периметр равен L стороны * N сторон, которое для квадрата равно 4 получим
P=4*sqrt(2)/2 = 2*sqrt(2)
Берем калькулятор, считаем, приблизительно получается 2*sqrt(2) = 2.828427 Это первое приближение снизу. Приближение сверху получить проще простого так как сторона внешнего квадрата равна диаметру, то 4*1=4, то есть имеем соотношение 2.828427 < Пи < 4 Это как бы давно известно и ничего нового тут я не открыл. Что же ускользнуло? А то, что отношение периметра к диагонали постоянно и не зависит от диагонали и периметра не только для окружности, но и для любого правильного многоугольника, в том числе и для квадрата. То есть для любого квадрата отношение периметра к диагонали можно выразить формулой
P=2*sqrt(2)*d
то есть можно сказать, что полученное число есть своего рода Пи квадрата, так далее и будем обозначать, пи(4)=2*sqrt(2) что приблизительно равно 2.828427 Число как можно заметить иррациональное, но алгебраическое (то есть вычислимое) а не трансцендентное (не вычислимое) как Пи окружности. Любое иррациональное число нельзя вычислить до конца (то есть получить рациональный эквивалент), оно бесконечно будет приближаться к этому эквиваленту, но никогда его не достигнет. Поэтому мы пользуемся рациональным приближением достаточной точности, например 2.83 если округлить до двух знаков после запятой или как поступаем с Пи округляя до 3.14 И в том и в другом случае уже заложена ошибка, и из природы сих чисел следует что невозможно абсолютно точно найти периметр квадрата по его диагонали или диагональ по стороне.
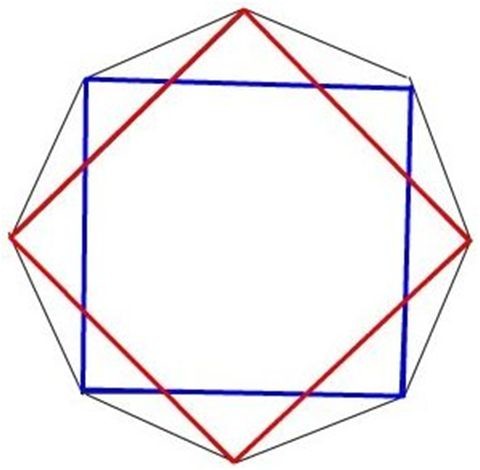
Далее продолжим делать ровно то же что и Архимед - нарисуем еще один квадрат повернутый относительно первого на половину угла, в данном случае угол квадрата 90 то есть на 45 градусов.
Соединим вершины квадратов (черная линия) и получим восьмиугольник, или многоугольник у которого число сторон равно 2^3 (квадрат это многоугольник с числом сторон 2^2) Аналогично поступим с внешним квадратом, в итоге они расположатся так
соответственно исследуемая окружность между ними (на рисунке не показана). Из рисунка видно, что треугольник AEF для двух квадратов никуда не делся и превратился в треугольник ABC, окружность по прежнему "зажата" между его вершиной B и основанием AC и проходит через точки A и C. Потом мы будем тем же методом увеличивать число сторон многоугольника кратно степени двойки (16,32,64 и т.д.) но это никаким образом не будет влиять на этот треугольник кроме как угол B будет становиться все более тупым и будет уменьшаться высота проведенная из вершины B на основание АС. У этого явления есть предел, но об этом позже. Пока же займемся периметром 8-и угольника. Есть простая универсальная формула для правильных многоугольников P=D*N*sin(180/N) но мы ей пользоваться не можем, ибо синусы углов не зная Пи не посчитать, а мы как раз таки Пи и ищем, то есть нужен иной подход. Поэтому вооружимся теоремой Пифагора и полезем в дебри:
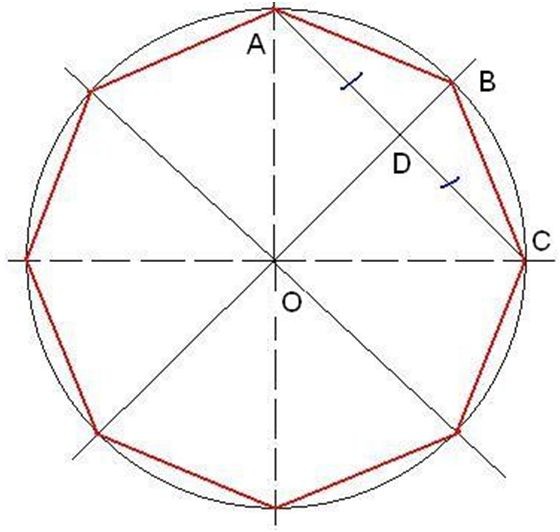
Итак, нам нужно как-то найти AB имея в наличии только AO (равно 1/2 по условию) и AC (длину стороны квадрата мы ранее вычислили - sqrt(2)/2) Так как отрезок OB делит AC пополам (мы проворачивали второй квадрат на половину угла квадрата) то AD тогда равен sqrt(2)/4. Этого достаточно чтобы через теорему Пифагора найти OD, а зная OD можно найти DB (OB также по условию равен 1/2) А зная DB можно через ту же теорему Пифагора добраться наконец таки до AB. Итак поехали:
OD^2 = AO^2-AD^2 = 1/2^2-(sqrt(2)/4)^2 = 1/4-2/16 = 2/8-1/8 = 1/8 тогда
OD = sqrt(1/8) = 1/sqrt(8) = 1/sqrt(4*2) = 1/(2*sqrt(2)) тогда
DB = OB-OD = 1/2-1/(2*sqrt(2)) = (sqrt(2)-1)/(2*sqrt(2)) и находим наконец таки AB
AB^2=AD^2+DB^2 = (sqrt(2)/4)^2+((sqrt(2)-1)/(2*sqrt(2)))^2 = 2/16+(3-2*sqrt(2))/8 = 1/8+(3-2*sqrt(2))/8 = (4-2*sqrt(2))/8 = (2-sqrt(2))/4 тогда
AB = sqrt((2-sqrt(2))/4) = 1/2*sqrt(2-sqrt(2))
Полученное значение AB также есть синус угла 180/8. Проверить так ли это можно например тут http://mathworld.wolfram.com/TrigonometryAnglesPi8.html
Тогда периметр восьмиугольника будет 8*1/2*sqrt(2-sqrt(2)) = 4*sqrt(2-sqrt(2)). Вооружившись калькулятором считаем, получается что-то около 3.0614674589 что есть рациональное приближение числа Пи для правильного восьмиугольника. Так и запишем, Пи(8) = 4*sqrt(2-sqrt(2)) ~= 3.06
Аналогичным образом находится сторона внешнего восьмиугольника, вывод приводить не буду (кто захочет - сам выведет), равна 8*(sqrt(2)-1) = 3.31370849898476 ~= 3.31
То есть мы удвоили число сторон и сузили коридор в котором находится Пи до 3.06<Пи<3.31
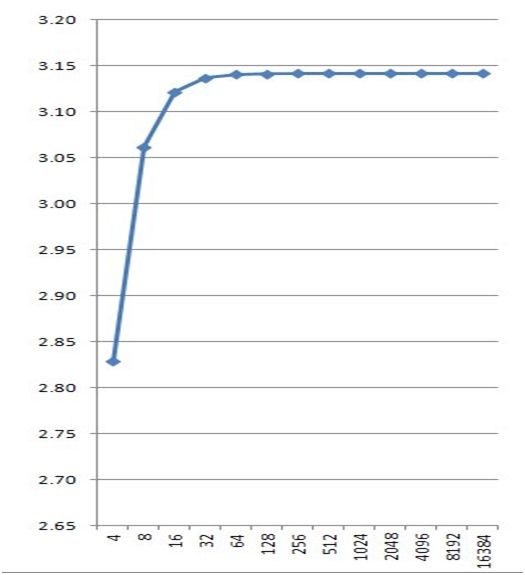
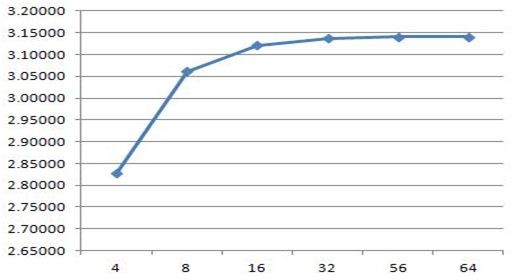
Аналогичным образом удвоив число сторон можно получить для внутреннего 16-и угольника Пи(16) = 8*sqrt(2-sqrt(2+sqrt(2)) а синус угла 180/16 соответственно 1/2*sqrt(2-sqrt(2+sqrt(2)) (убедиться в этом можно тут http://mathworld.wolfram.com/TrigonometryAnglesPi16.html) Еще раз удвоив число сторон можно придти что синус 180/32 = 1/2*sqrt(2-sqrt(2+sqrt(2+sqrt(2))) и Пи(32) соответственно 16*sqrt(2-sqrt(2+sqrt(2+sqrt(2))) Проверить можно тут http://mathworld.wolfram.com/TrigonometryAnglesPi32.html Можно и далее идти этим путем, а можно посмотрев на закономерность развития этой формулы придти к простому выводу, что каждое увеличение степени двойки числа сторон на единицу приводит к дописыванию еще одного вложенного квадратного корня из 2. Устремив степень в бесконечность как бы можно в конце концов найти Пи. Я что-то новое открыл? Нисколько. Я всего лишь вывел давно известную формулу Виетта https://en.wikipedia.org/wiki/Vi%C3%A8te%27s_formula и лишь наглядно показал ее геометрический смысл - каждый N угольник в любой подобной формуле имеет свое алгебраическое значение Пи в отличие от Пи окружности, которое трансцендентное. Тогда по сути Пи не есть константа, а некая функция, и вполне можно построить ее график. Например так
По графику видно, что чем больше число сторон тем выше значение пи, то есть например пи 50-и угольника будет находиться где-то между пи 32 и пи 64. Поскольку любое рациональное приближение Пи окружности по сути есть использование Пи(n) n-угольника, да и еще и неправильного, так как все Пи в данном ряду - иррациональные. Для интереса найдем чему соответствует привычное приближение 3.14 Для этого придется решать уравнение вида sin(180/n)=Пи(окр)/n которое было решено итерацией. Получилось, что 3.14 это на самом деле многоугольник с числом сторон где-то между 56 и 57. То есть мало того что 3.14 это далеко не окружность, это еще и неправильный многоугольник с числом сторон 56 при этом одна из сторон уходит за границы окружности, так как фигур с дробным числом сторон не существует. Добавим и ее на график и обрежем по Х число углов до 64 так как все выше растет очень медленно и на графике фактически прямая:
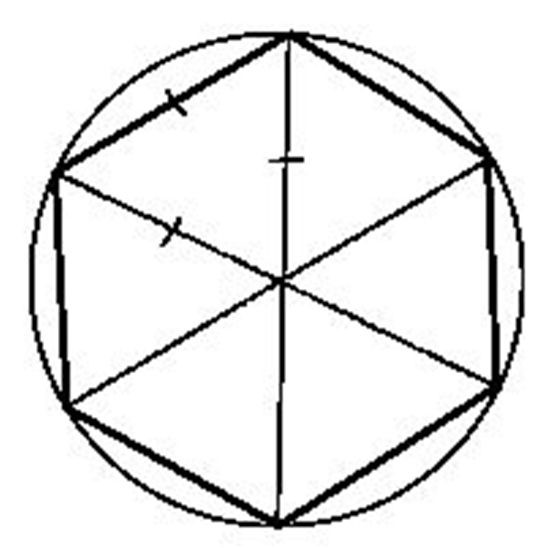
Итак что еще осталось не исследованным? N<4 и другие ряды, не по степени двойки. Лезть туда особого смысла нет, ибо полученные значения лягут между значениями двоичного ряда и нет необходимости в построении непрерывного графика для любого N. Интерес представляет только N=3 и N=6 вот с ними и разберемся. N=3 это вписанный равносторонний треугольник. Путем аналогичных для квадрата построений получим что для N=3 Пи(3) равно 3*sqrt(3)/2 если его посчитать на калькуляторе получается что-то около 2.59807621 или приблизительно 2.6 Далее аналогично повернем треугольник на 60 градусов и по вершинам построим шестиугольник.
Без всяких лишних построений очевидно, что правильный шестиугольник состоит из 6-и равносторонних треугольников и у него соотношение периметра к диагонали равно ровно 3. Это единственный из всех многоугольников, для которого Пи - рациональное число. Можно также предположить, что для N=2 получим отрезок совпадающий с диаметром, то есть пи(2)=1, для N=1 получим уже как минимум радиус (тогда пи(1)=1/2) и для N=0 имеем всего лишь точку, у точки размер 0, а ноль на что ни дели все равно будет 0. То есть пи(0)=0. Добавляем все это в график и смотрим что получилось
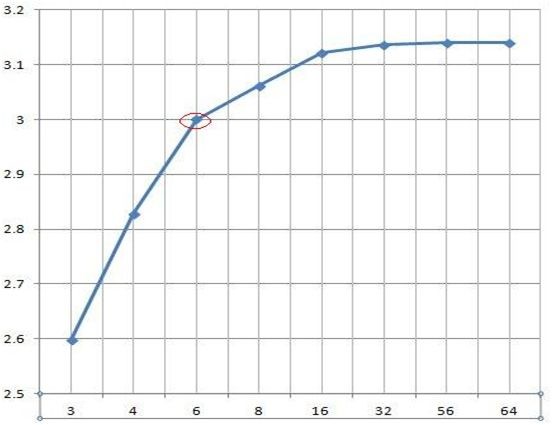
Судя по тому что для N<3 имеем явный разрыв и изменение поведения функции, мои рассуждения про фигуры с N<3 несправедливы и само собой таких фигур не существует. То есть функция начинается с N=3 и до бесконечности, так и нарисуем ограничив N до 64
Итак, мы имеем множество иррациональных чисел, которые до того как представлены рациональными эквивалентами являются значением пи соответствующего многоугольника и одну единственную фигуру (правильный шестиугольник) для которой пи рациональное целое число. Этим как раз таки и объясняется, почему окружность легко и абсолютно точно можно поделить на 6 частей. Но 6 это 2*3, исходя из этого окружность также легко делится пополам (просто проводим прямую через центр) и из 6-и угольника также легко выделяется вписанный равносторонний треугольник. Если следовать этому, то окружность можно один раз поделить на 3 и потом делить что получилось на два и еще раз на два и так далее либо делить на два сколько угодно раз и потом что получилось можно будет один раз разделить на 3. То есть если разложить такое на простые множители, то получим 3*2*2*2*... и т.д. В этом разложении не присутствует вторая тройка (что имеет место при делении на 360) а также нет 5-ки (что имеет место при делении на 360 и 400). Этим как раз и можно объяснить, что для некоторых значений углов есть алгебраические (пусть и иррациональные) значения тригонометрических функций а для некоторых углов можно лишь найти рациональное приближение и по сути значения тригонометрических функций для таких углов также трансцендентные. Если делить окружность согласно множителей 3 и 2, то ближайшее похожее на привычные нам 90 градусов будет 96 (3*2*2*2*2*2) и вся окружность тогда будет не 360 а 384 градуса. Это первые грабли, на которые наступили древние и которые вручили нам, с чем и маемся. Если делить окружность на 384 а не 360 градусов (и далее доли не в десятичной системе и не минутах секундах и прочей фигне а кратно двойке), то значение любых тригонометрических функций любого такого угла будет алгебраическим.
С Пи вроде бы как разобрались, и я наглядно показал, что используя любое рациональное приближение, пусть хоть с миллионом знаков после запятой, мы на самом деле используем пи какого-то многоугольника, пусть даже и с очень большим числом сторон, и к тому же еще и неправильного. То есть, фактически, вычисляя Пи окружности с точностью в миллион знаков после запятой мы ищем не константу а предел функции, график которой я привел. Осталось теперь разобраться, а что же такое окружность? Лезем на вики и читаем определение https://ru.wikipedia.org/wiki/%D0%9E%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D1%8C Определений там множество, я возьму самое первое и оно меня вполне устраивает: “Окру́жность - это фигура, которая состоит из всех точек на плоскости, равноудаленных от данной точки. Эта точка называется центром окружности”. Очевидно, что многоугольник даже с большим числом сторон этому определению не удовлетворяет и окружностью считаться не может. Попробуем поискать, где же эта самая окружность прячется, параметры которой удовлетворяют определению. Возьмем для наглядности тот же чертеж с двумя квадратами:
В математическом анализе обычно когда ищут предел чего либо, то что-то фиксируют а что-то устремляют в бесконечность и смотрят что получится. Когда ищут Пи и пределы с ним связанные обычно фиксируют диаметр окружности (принимая его за 1) и устремляя в бесконечность N числа сторон многоугольника. Я сделаю немного иначе - зафиксирую основание EF треугольника AEF и буду устремлять в бесконечность диаметр окружности и число N разбиений. Как было показано выше, при таком построении описанного и вписанного многоугольников окружность всегда проходит через такой треугольник и его два угла, при увеличении числа разбивок меняется только высота треугольника. С ростом числа разбиений высота такого треугольника стремится к нулю и при бесконечном N вершина А сольется с основанием EF. но так как не существует треугольников, у которых сумма двух сторон равна третьей стороне (само собой я оперирую евклидовой геометрией), то мы получим что окружность выродилась в прямую. Но мы же знаем что прямая это не окружность.... она типа бесконечна и не имеет ни начала ни конца... а с другой стороны, что мы вообще знаем про прямые? Итак, берем листок на котором с самого начала рисовали прямую и окружность и смотрим еще раз что мы там нарисовали... внимательно... Мы нарисовали прямую? Нет. Мы нарисовали по сути отрезок. Можно конечно же нарисовать прямую так, что она будет занимать весь лист. Ну и что? Это опять отрезок. Только ограничен физическими размерами листа. Попробуйте нарисовать бесконечную прямую. Не выйдет, ибо мы с вами существа имеющие вполне конечные размеры, на конечных размеров планете живущие и доступна нам далеко не вся бесконечная Вселенная. Выходит, мы никогда не имели дело с истинной прямой, а всегда оперируем отрезками. А я тут взял и вывел вдруг, что прямая суть фрагмент окружности бесконечного диаметра. А где мы имеем такие прямые? О! Да наше евклидово пространство трехмерное да ось координат ХYZ, как раз по сути оно и есть... Ну что еще не бесконечно, как пространство в котором мы находимся? Но если оно бесконечно, даже двигаясь по прямой бесконечно долго вы все равно вернетесь в ту точку откуда и начали движение. А если будете менять направление то в ту же точку не вернетесь, но все равно за пределы пространства не выйдете, ибо оно как бы само в себя свернуто в этакую "суперсферу", в которой нет ни входа ни выхода за ее пределы... Продолжим анализ далее. Итак, физики утверждают, что Вселенная которую мы видим и в которой живем развернулась из точки сингулярности, вместе с пространством временем и всем что ее наполняет. Но тогда можно предположить, что то что нам кажется бесконечным таковым все же не является. То же пространство, если оно развернулось из точки, что мешает продолжать ему непрерывно расти далее? Предположим что гипотеза что пространство свернуто в окружность по любому из направлений верна и скорость роста пространства меньше скорости света. Что получим тогда? Свет от нашей галактики идет как в ту сторону что смотрит наблюдатель, так и в обратную. Сделав такой "круг", он опять вернется в ту же точку, но уже со стороны куда смотрит наблюдатель. Но так как расстояние пройдено огромное, дошедший луч будет ничтожно мал и слаб. Но астрономия на месте не стоит, и вот навели Хаббл на пустое место на небе, сделали увеличение побольше да выдержку подольше и что там увидели? Множество самых разных галактик и туманностей которым нет числа... И сделали вывод что количество материи во Вселенной бесконечно. Количество звезд бесконечно. Но если это так, то мы тогда должны видеть равномерно засвеченное небо а не зияющую черноту с редкими вкраплениями звезд. Чтобы как-то сей факт объяснить, придумали наличие темной материи да темной энергии которые этот свет поглощают. А на деле мы может быть имеем дело со своего рода "трельяжом" только космических масштабов и в нашей Вселенной вполне конечное количество звезд, галактик и вещества. Намного меньше чем нам сейчас кажется.
Если кто не знает, трельяж это зеркало состоящее и неподвижного и двух створок, как например на этой картинке
Если створки сомкнуть и внутрь такого зеркала посмотреть, то можно увидеть отражение себя любимого бесконечно уходящее вдаль. Но так как зеркало не идеальный отражатель света, то обычно видно первые N переотражений. И сколько их видно зависит от освещенности, качества зеркала и остроты зрения наблюдающего.
Но это еще не все. Первое условие которое вижу я, для того чтобы построить окружность удовлетворяющее ее научному определению - бесконечно большой диаметр как и сама окружность. То есть в "истинной бесконечности" вы окружность построите. А в нашем конечном мире - не получится. Попробуем с этим разобраться и заодно поискать нижний предел выполнения условия. Ведь как-то мы их тем же циркулем рисуем ведь? Итак снова берем листок бумаги и смотрим на "окружность". Пытаемся понять, а что же в ней не так? Не видно? Берем лупу и смотрим. Не помогло? Карандаш был очень тонкий и циркуль очень качественный, да такой что нарисовали линию атомарных размеров? Тогда берем "электронный микроскоп" или просто напрягаем воображение и пытаемся понять, что у нас получится если минимальная единица такой окружности - атом. А можно не напрягаться и вспомнить, как рисовались окружности из бейсика на экране первых компьютеров. Тогда с разрешением экрана было туго и точки были крупные и хорошо различимые. Что там получалось? Окружность? Или некоторая кривая "лесенкой", на окружность только похожая? Сейчас с разрешением экранов стало получше и мы зернистости не видим, но возьмите лупу - она куда-то делась? Просто стала мельче и незаметней. Зернистость размером в атом нам совсем не видна и даже в самые лучшие микроскопы, но мы знаем что атом имеет конечные размеры, это давно доказано. Следствие сего - вы никогда в мире состоящем из конечных атомов не сможете построить идеальной окружности как в определении. На проверку это обязательно окажется некая кривая, состоящая из отрезков, которая окружностью только кажется. Каково тогда условие чтобы мы видели или смогли построить идеальную окружность? Оно простое и очевидное - при условии что наша материя состоит из бесконечно малых точек, размер которых не измерить и не описать. То есть мы либо должны залезть во вселенную и строить окружность бесконечно больших размеров, либо влезть на "самое дно" микромира и пытаться построить ее там предполагая что это “дно” бесконечно мало и бесконечно равномерно. Но мир атомов состоит из конечного размера частиц, они не однородны, состоят из других более мелких, которые также конечны и не однородны, и как этим не оперируй идеальной окружности не получится. Так почему тогда математики не могут найти Пи окружности и считают его трансцендентным? Потому что в нашем конечном мире, состоящем из конечных сущностей, не существует такой фигуры как окружность. Это фигура из области бесконечности, только там может существовать и только там Пи - вещественное число, хоть и бесконечно большое. Так откуда мы тогда знаем про окружность? Да от тех же древних. С истории изобретения колеса. Далее открыли что планеты вокруг Солнца по орбитам близким к окружности летают, и сами Солнце да планеты имеют форму сфер. Посчитали с приемлемой точностью для нашего конечного мира и решаемых задач Пи, вывели формулы тригонометрии, построили кучу теорий многое объясняющих (и не менее многое запутывающих), пользуемся, привыкли и в аксиомы не лезем ибо делать там нечего. Далее следует простой вывод о граблях, на которые мы наступили и которые называются "мышлением по аналогии": Вот мы привыкли что планеты вокруг Солнца летают, а так как размеры их и радиусы орбит много больше размеров атомов, приняли что это все равномерные окружности, забили в формулы, получили хорошее совпадение результатов, приняли за истину и успокоились. Далее физики влезли в атом, нашли что там есть ядро, что оно тяжелое и в центре, что по орбитам летают электроны, но посмотреть на это никак нельзя, осталось только вообразить. Что вообразили? По аналогии с планетами солнечной системы резерфордовскую планетарную модель атома. Что электроны летают вокруг атомов по круговым орбитам. Но тут всплыло, что электрон двигаясь по такой орбите будет излучать энергию, а значит терять импульс и упадет на ядро. Что атом так существовать не может. Пришлось спасать теорию и придумывать запрещенные уровни, на которых электрон находиться не может, а может только на разрешенных. Так называемых орбиталях. И может переходить только из одной орбитали в другую. Но так как при этом энергия меняется скачком, то выползла квантовая физика и все что за ней последовало. Почему квантами – никто не знает. Почему не может в запрещенной орбитали находиться? Неизвестно. Табу. Кто-то запретил, например Создатель, так и существует, нам остается только пользоваться. Про то как электрон с орбиты на орбиту скачком переходит я отдельно пройдусь. Представьте, что Земля вот так в миг со своей орбиты перешла на орбиту Марса а потом обратно. Не получается? Она же массу какую имеет, инерцию, это сколько энергии в миг нужно ей сообщить/отобрать чтобы она так скакала? Бесконечно много, так как время перехода равно нулю. Электрон не Земля, весит поменьше, но все же массу имеет, а значит и свой импульс и свою инерцию. И вот нам приспичило его разогнать чтобы он влез на орбиту повыше. Ну там фотон прилетел побеспокоил. В планетарной модели такое движение перехода с орбиты на орбиту должно быть линейным. А нельзя, квантовая механика порушится вместе со всеми теориями что на ее фундаменте стоят. А что он тогда делает, этот электрон? А телепортируется. И туннельный эффект туда же в ту же область. Вот что получается, когда мы по аналогии, привычные нам понятия макромира пытаемся натянуть на происходящее в микромире и этим как-то суть процессов в нем объяснить. А микромир то совсем иной. И единственная "лупа" которой туда еще можно влезть это математический анализ. Или просто математика. А у нас в этой лупе блохи завелись... что мы тогда увидим? Итак, исходя из того что я вывел для окружностей логично следует то, что электрон не может летать вокруг ядра по круговым орбитам. В силу того, что нет для него такой геометрической фигуры как окружность. Значит будет летать по иным траекториям, сходным с каким то из многоугольников. Из правильных, иначе энергию терять будет да упадет на ядро. Допустим по квадрату. О том что эта гипотеза похожа на правду говорит тот факт, что многие вещества склонны образовывать кубические кристаллические решетки. Чего бы им не стремиться к шару как все жидкое в макромире? Зачем им энергетически более избыточные структуры? А потому что таковы траектории их электронов и суммарный вклад приводит к тому, что соседним атомам проще выстроиться в такую решетку нежели с ней бороться и быть аморфным. Но простите, резкий поворот на 90 градусов это тоже приложение импульса согласно ньютоновской механике, попробуйте вы в макромире например авто на 100км/ч под прямым углом в поворот вписать. Не выйдет, перевернетесь. А электрон чем хуже? А вот тут похоже (моя гипотеза) придется забыть все что мы знаем про частицы и в качестве таковой электрон не рассматривать. Электрон это по сути конгломерат энергетических полей, суть и природа которых нам непонятна и недоступна. Мы знакомы с немногим из того что возможно есть - электричество магнетизм да гравитация. И то уже знаем, что та же электромагнитная волна (фотон например) при движении поочередно переходит из электрического поля в магнитное и наоборот. Есть точки где он целиком магнит. Есть где целиком заряд. Векторы этих полей всегда расположены под углом 90 градусов то есть имеет место переход энергии из одного вида поля в другой. Возможно что-то похожее происходит и с электроном - он двигаясь непрерывно взаимодействует через электрическое поле с ядром. Двигаясь по прямой вдоль ядра он теряет импульс, его энергия переходит в иной вид поля, повернутого под 90 градусов к текущему, при исчерпании импульса направление движения меняется. Тогда если вдруг "побеспокоил фотон" то его импульс складывается с тем что есть, движение по прямой продолжается далее, выходим на новую орбиту и там движемся аналогично. Но при этом возникает также и импульс приложенный через электрополе к ядру, что приводит к его смещению в пространстве, сам атом приходит в движение, сталкивается с другими, в итоге такого взаимодействия электрон опять отдает фотон и возвращается на прежнюю орбиту. И никакой мистики со скачками да туннелями, там скорее всего и понятий (опять же из нашего микромира) о непроницаемых барьерах ака стенка о которые электрон может биться и не пробить и близко нет. А что есть - никаким микроскопом не подсмотреть. Только математика. Но тут начинаются такие дебри, в которые лезть мне с моими скромными познаниями нет никакого смысла... Посему если сие вдруг дойдет до толковых физиков/математиков и они не сочтут сие бредом, то пусть они дальше морщат лоб и разбираются со своими теориями :)







282 комментария
9 лет назад
Удалить комментарий?
Удалить Отмена7 лет назад
Удалить комментарий?
Удалить ОтменаУдалить комментарий?
Удалить Отмена