Как закон первой цифры способен выявить обман и мошенничество

"Открытие" было странным и доказать Ньюкомб его не смог. О нем забыли на полтора века, пока в 1938 году, на этот же феномен не обратил внимание инженер и физик Френк Бенфорд.

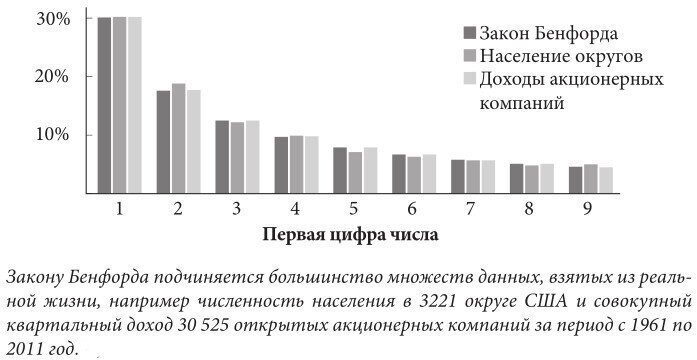
Его изучение массивов данных было более детальным - он проанализировал 20 таблиц, содержащих сведения о 335 рек, удельной теплоёмкости и молекулярном весе тысяч химических соединений, номерах домов 342 улиц. Это доскональное изучение выявило, что единица является первой значащей цифрой с вероятностью не 1/9, как следовало ожидать, а около 1/3.

Но получался бред какой-то. Ведь согласно теории вероятности любая цифра должна встречаться с той же регулярностью, что и единица.

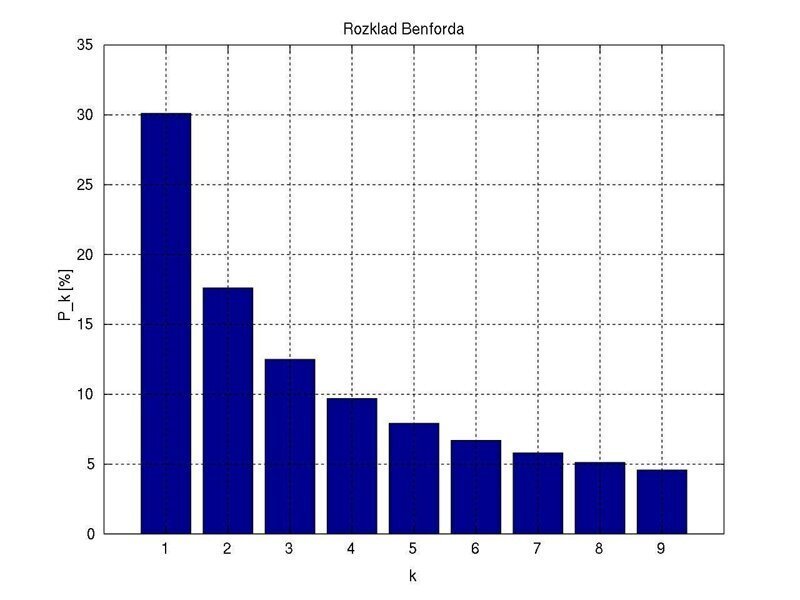
Таким образом появился закон Бенфорда или закон первой цифры, который гласит, что в таблицах чисел, основанных на данных источников из реальной жизни цифра "1" на первом месте встречается гораздо чаще, чем все остальные (приблизительно в 30 % случаях), а также вероятность того, что цифра будет стоять на первом месте в числе тем больше, чем меньше цифра.

Перенося закон Бенфорда в реальную жизнь, его можно объяснить так: в мире маленьких вещей всегда больше, чем больших: маленьких водоемов больше чем больших, маленькие камни встречаются чаще, чем большие валуны, серьезные аварии случаются реже, чем незначительные. В итоге, после всех исследований Бенфорд не только сформулировал закон преобладания единицы, но и вывел формулы, которые позволяют рассчитать частоту появления каждой цифры в начале числа в том или ином числовом массиве.

Простой пример из жизни: мы вносим в банк 1000$, под 10 % годовых. В следующем году вклад вырастет на 10% и будет составлять уже 1100$, еще через год на счету будет уже 1210$, затем 1331$ и так далее. Единица остается первой цифрой нашего баланса на счете в течение долгого времени. Когда счет будет составлять 2000$, двойка первой цифрой будет оставаться уже в течении более короткого периода. Когда депозит составит 9000$, 10-процентный рост приведет к росту суммы вклада свыше 10000$, и единица снова долгое время будет оставаться первой цифрой. Таким образом, эти изменения чисел подчиняются закону Бенфорда: все, что растет в числе, размере, весе или цене дольше всего остается в «области единицы».

И более того, оказалось, что закону Бенфорда подчиняется и некоторые математические объекты, такие как факториалы, числа Фибоначчи или последовательность степеней двойки.

Долгое время математики сомневались в справедливости закона Бенфорда. Во многом это объяснялось приверженностью к неподкупным законам теории вероятности, для которой все цифры одинаковы. Но сторонники Бенфорда утверждали, что при подсчете необходимо обращаться не к математической абстракции, а к конкретным примерам реальной жизни.

В 1986 году ученый- физик Дон Лемос обратил внимание на понятные каждому человеку факты: луж оказывается гораздо больше чем прудов. Количество прудов тоже значительно больше чем озер, зато число озер превышает количество морей, которых в свою очередь также значительно больше, чем океанов. Так же вполне логично, что озер с площадью зеркала от 1 до 2 километров квадратных значительно больше, чем тех чья площадь зеркала находится в рамках от 8 до 9 квадратных километров. И уж совсем очевидно, что мелкой гальки гораздо больше, чем крупных валунов.

Что самое интересное, у этой "нелогичной" теории есть вполне практическое применение. Группа интернациональных ученых рассмотрела, как закону Бенфорда подчиняются природные процессы, такие как продолжительность времени между геомагнитными инверсиями, выбросы парниковых газов, число инфекционных заболеваний. Сегодня наиболее полно исследована возможность примениния закона первых чисел в геофизике.

Исследования проводились в Перу и Канберре. В Перу ученые обнаружили, что незначительное вертикальное смещение поверхности земли не удовлетворяет закону Бенфорда, но сдвиги, вызванные мощными землетрясениями, напротив соответствуют закону. Ситуация с сейсмической активностью в Канберре была аналогичной, лишь несколько отличалась степень соответствия закону во времени. Эти исследования, по мнению математика Теодора Хилла, не принимавшего участия в работе, будут иметь огромное значение в будущем, так как с помощью закона Бенфорда станут отбирать модели физических процессов.

Но более всего закон Бенфорда оказался действенным в экономике. В частности, в проверке финансовой отчетности.

В конце 20 века американский математик Марк Нигрини пришел к выводу, что подчиняться закону Бенфорда должны и цифры в налоговых декларациях, соответственно несовпадение с законом первой цифры указывает на подтасовку данных. Разрабатывая эту теорию, Нигрини проанализировал более 200000 налоговых деклараций и опытным путем доказал, что почти в каждое третье число в аутентичных отчетах начинается с единицы.

На основании этих данных математик разработал программу для проверки числовых массивов на соответствие закону Бенфорда. В 1995 году эта программа была протестирована. В ходе этого испытания Нью-йоркская налоговая полиция разоблачила семерых мошенничающих налогоплательщиков. Данная программа получила название «Digital Analysis» (сейчас особенно активно использует эту программу мировая компания «Ernst & Young»). На данный момент известно около десяти тестов «Digital Analysis».

Наиболее распространены из них следующие шесть.

1. Анализ частоты первой цифры. В данном случае используется непосредственно сам закон Бенфорда.

2. Анализ частоты первой и второй цифры. При использовании данного теста отдельно проверяется частота цифры от 1 до 9 на первой позиции и частота цифры от 0 до 9 на второй. Затем составляется таблица соответствий, которая анализируется на отличие частоты цифр в приведенной последовательности от эталонной последовательности Бенфорда.

3. Анализ дублей. Данный метод опирается только на методологию Бенфорда, а не на сам закон. Данная проверка выявляет частоту числовых повторов в большом количестве документации. Все повторяющиеся числа в исследуемых данных сортируются по читстоте повторов, а затем проверяются уплотнения повторов ряда чисел. Наиболее часто анализ дублей используют для налоговых проверок, при внутренних расследованиях и внешнем аудите.

4. Анализ первой пары цифр. Этот метод фактически представляет собой усовершенствованный второй тест, так как он исследует частоту появления цифр в начале числа не от 1 до 9, а от 10 до 99. Наиболее удобно использовать этот метод в его графической интерпретации.

5. Анализ первой тройки цифр. Метод, более точный в сравнении с первым, вторым и четвертым тестами. Программа анализирует частоту первой тройки цифр от 100 до 999 в изучаемой числовой последовательности. Данный метод используют при проверке большого объема информации (от 10000 значений).

6. Анализ округлений. Тест проводится для проверки частоты последних значащих цифр анализируемой числовой последовательности. Тест позволяет выявить несоответствующую эталону закона Бенфорда частоту постоянного округления в большую или меньшую сторону.

Нигрини даже забавы ради проанализировал налоговые декларации четы Клинтонов, которая оказалась честной семьей налогоплательщиков.

Помимо налоговых деклараций еще одной сферой применения закона Бенфорда на практике является возможная подтасовка голосов на выборах, поскольку данные о них также определяются большим массивом бюллетеней.

Так или иначе, но закон первых чисел не имеет юридической силы. И если вычисления по формуле Бенфорда выявляют нестыковки, допустим, в заполненных налоговых декларациях, то в таком случае подобные бумаги автоматически становятся целью повышенного интереса для аудиторов.