Что такое гиперпространство?
«Лететь через гиперпространство – это тебе не на ферме урожай собирать, малыш! Без точных вычислений мы можем пролететь сквозь звезду или оказаться слишком близко от сверхновой, и на этом наша поездка закончится навсегда, ясно тебе?» (Хан Соло – Люку Скайуокеру)
Что значит «гипер»?
Писатели-фантасты и создатели фильмов во все времена очень любили учебники по математике. Уж больно много там крутых и загадочных слов («бифуркационная поверхность эллиптической омбилики» – ух!) – самое то, что нужно для того, чтобы увлечь любознательного читателя!
По-древнегречески приставка «гипер-» («ὑπέρ») означает «над, сверху, выше» – а в большом и взрослом учебнике математики мы можем встретить десятки самых разных терминов с этой приставкой. И «гиперповерхность», и «гиперплоскость», и «гиперсфера», и «гиперкуб» (см. рисунок) – и, конечно же, «гиперпространство». В общем, слово взято из математики. Но что же оно означает?
Эту фигуру математики называют "гиперкуб". На самом деле увидеть ее целиком невозможно это только одна из возможных проекций
Если без формул, то «гиперпространство» означает некое многомерное «над-пространство», «супер-пространство», в котором наше с вами привычное пространство (влево-вправо, вверх-вниз, вперёд-назад) является только маленькой его частью.
Сперва это не умещается в голове: ведь наша Вселенная, наше пространство – оно же бесконечное? Как же бесконечность может быть «частью» чего-то другого? В реальном мире представить такое действительно трудно. На такие фокусы способна только математика – или же научная фантастика!
Складки и тоннели
В чём главный секрет гиперпространства? В том, что внутри него наше пространство – то, которое нам кажется идеально «ровным» и «прямолинейным» – может оказаться сильно искривлённым, свёрнутым в причудливые «складки». То, что нам кажется прямой линией с огромным расстоянием между точками А и В, в гиперпространстве может вдруг оказаться «свёрнутым» так, что расстояние и время путешествия оказываются короче в миллионы раз!
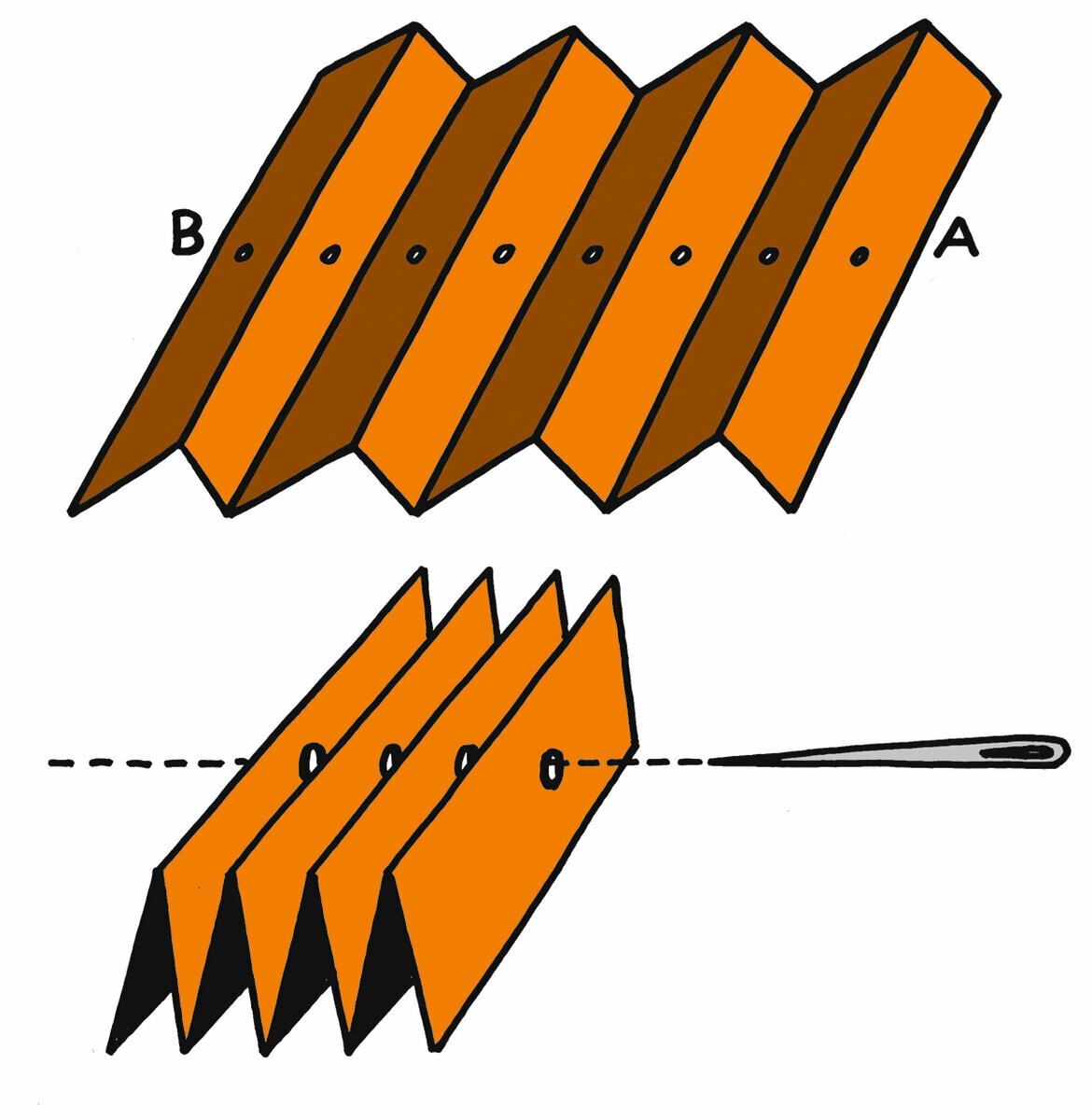
Простой опыт: как сократить расстояние между точками А и В на плоскости, то есть в двухмерном пространстве? Нужно "добавить" ещё одно измерение.
Вы знакомы с игрушкой «прозрачный лабиринт»? В ней нужно прогнать маленький шарик из одного угла стеклянного кубика в другой – сквозь систему запутанных «тоннелей» и «этажей». С первого раза сделать это ого-го как трудно, можно потратить не один десяток часов! А теперь представьте себе, что гиперпространство – это наш мир, игрушка-куб – «обычное пространство», шарик – «корабль», и где-то там, «внутри обычного пространства» шарика, извилистый путь через лабиринт представляется длинной прямой линией – скажем, это маршрут полёта корабля от одной звезды к другой... Тогда в нашем «гиперпространстве» мы можем «сжульничать»: снять с кубика прозрачную стенку (то есть «прыгнуть в гиперпространство»), переложить шарик («корабль») в другой угол – и вуаля! «В любую точку вселенной – за 5 секунд!».
Обходя напрямую «складки», «повороты», «тоннели» и другие структуры нашего пространства внутри гиперпространства, опытный пилот может за несколько дней или недель пролететь расстояние, на преодоление которого в реальном пространстве ушли бы миллиарды лет...
Так не бывает?
Или всё-таки бывает? Иногда бывает...
Когда мы сидим в классе за партой или играем во дворе, наша Земля представляется нам плоской, «прямой», не так ли? Но на самом деле она – шар, её поверхность искривлена! Если мы возьмём маленькое расстояние – скажем, от одного края стола до другого или даже от дома до школы, это искривление останется для нас незаметным, «пренебрежимо малым», как говорят математики. Но если взять расстояние побольше? Вот тут-то и начинаются сюрпризы.
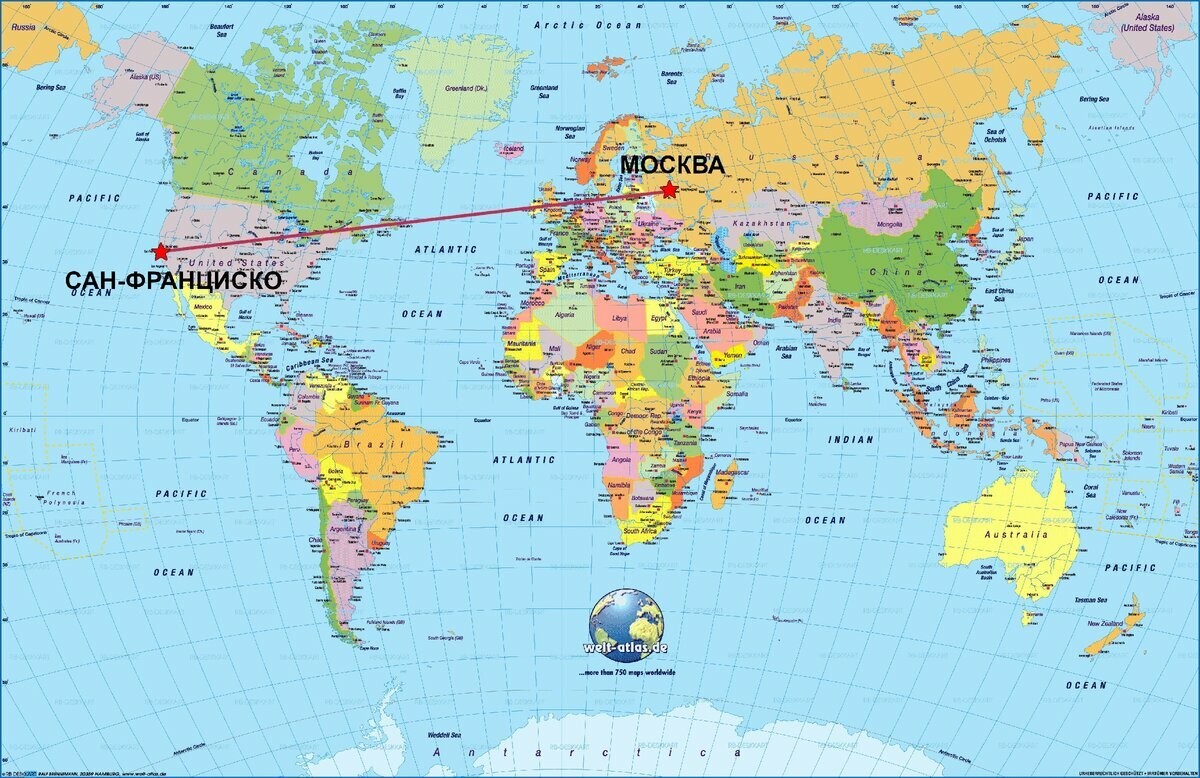
Допустим, мы решили измерить расстояние «по прямой» от Москвы до Сан-Франциско. Нет ничего проще – берём карту, проводим по линейке прямую, переводим миллиметры в километры с помощью указанного на карте масштаба и получаем расстояние – 12 тысяч километров. На карте видно, что наш маршрут лежит через Литву, Данию, Великобританию, Ирландию, остров Ньюфаундленд, озёра Гурон и Мичиган, штаты Айову, Небраску, Колорадо, Юту и Неваду.
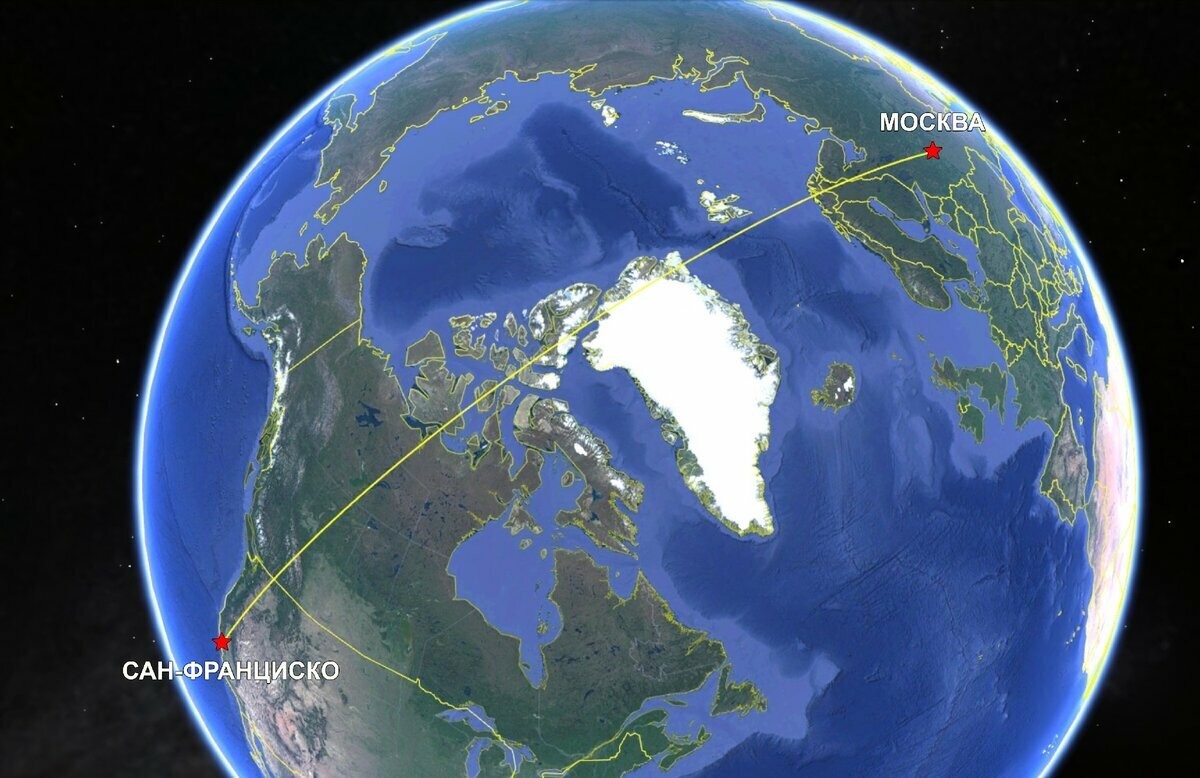
Но давайте проверим наши измерения на глобусе. Туго натянем нитку между Москвой и Сан-Франциско... Мамочки! У нас получается совершенно другой маршрут! Он будет пролегать через Карелию, Норвегию, к западу от Шпицбергена, северную Гренландию, остров Элсмир, остров Виктория, Большое Невольничье Озеро, штаты Альберту, Вашингтон и Орегон. А расстояние при этом получится 9500 километров! На 2 с половиной тысячи километров меньше, то есть «быстрее»!
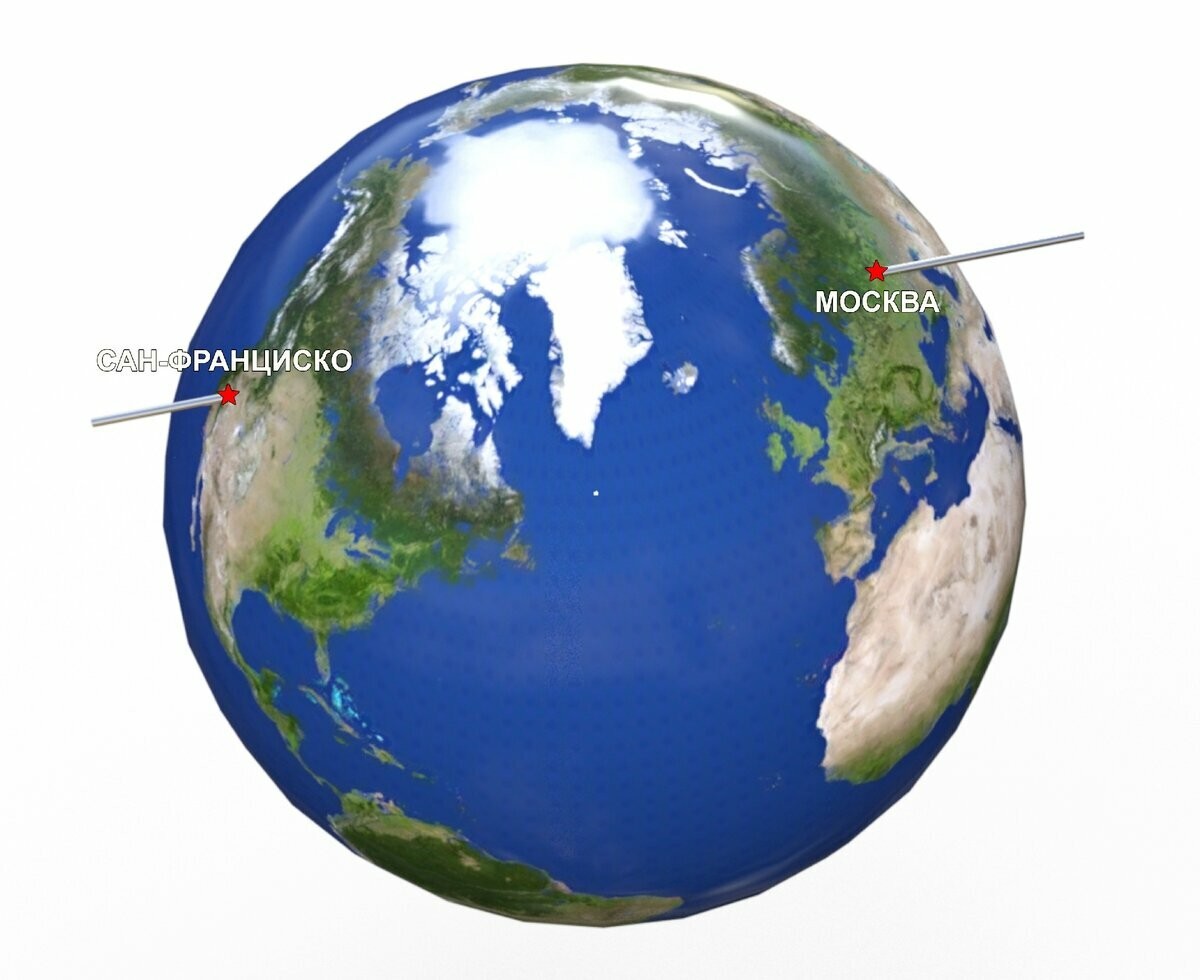
Однако это ещё не самый быстрый и прямой путь! Самый быстрый и прямой мы получим, если «проткнём» наш земной шар гигантской воображаемой спицей, проделав под его поверхностью тоннель от Москвы до Сан-Франциско. Максимальная глубина залегания этого тоннеля составит 1700 километров, а длина будет всего лишь... 8500 километров! Ещё на одну тысячу километров меньше!
Как видите, даже в нашем реальном мире «длина по прямой линии» может сильно изменяться в зависимости от того, что именно мы называем прямой– и «прямая» на карте может оказаться очень даже «кривой» в реальности. 3 с половиной тысячи километров – согласитесь, солидная разница в расстоянии. А что уж говорить о фантастическом гиперпространстве...
Источник:





38 комментариев
3 года назад
Удалить комментарий?
Удалить Отмена3 года назад
Удалить комментарий?
Удалить Отмена3 года назад
Удалить комментарий?
Удалить Отмена