Уравнение Эйлера

«Как сонет Шекспира схватывает саму суть любви, или картина показывает внутреннюю красоту человека, уравнение Эйлера проникает в самые глубины существования»

Математик из Стэнфорда Кейт Девлин (Keith Devlin) написал эти слова об уравнении в эссе 2002 года, которое называлось «Самое прекрасное уравнение». Но почему от формулы Эйлера перехватывает дыхание? И что она вообще значит?

Во-первых, буква «e» представляет собой иррациональное число (с бесконечным количеством цифр), которое начинается с 2.718281828459045… Открытое в контексте непрерывно начисляемого сложного процента, оно описывает темпы экспоненциального роста от колоний популяций насекомых до радиоактивного распада. В математике число обладает рядом неожиданных свойств, например, оно равняется сумме обратных факториалов от нуля до бесконечности. В конечном счете, константа e оккупировала математику, взявшись вроде бы ниоткуда, но оказавшись в большом числе важных уравнений.

Далее. i представляет собой так называемую мнимую единицу – квадратный корень из минус 1. «Так называемую», потому что в реальности не существует числа, которое, будучи умноженным само на себя, в результате дало отрицательное число (потому отрицательные числа не имеют действительных квадратных корней). Но в математике существует большое количество ситуаций, когда приходится извлекать квадратный корень из отрицательного числа. Число i используется как своеобразная пометка того места, где такая операция была произведена.

Пи – отношение длины окружности к ее диаметру, одна из любимых и наиболее интересных констант в математике. Подобно e, она появилась в большом количестве математических и физических формул как будто из ниоткуда.

Константа e, возведенная в степень мнимая единица, умноженная на Пи, равняется минус одному. Из уравнения Эйлера следует, что добавление к этому единицы дает ноль. Трудно поверить, что все эти странные числа, одно из которых даже не относится к реальному миру, могут быть так просто скомбинированы. Но это доказанный факт.

#интересное #математика #уравнение эйлера

Fishki в Телеграм

Посты на ту же тему

Я немного завидую медведю (ассорти)

Высшая математика для гуманитариев

Новорожденные животные

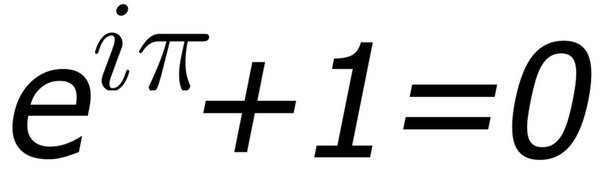
68 комментариев

Правила

!!! Оскорбления в комментариях автора поста или собеседника. Комментарий скрывается из ленты, автору выписывается бан на неделю. Допускаются более свободные споры в ленте с политикой, но в доступных, не нарушающих УК РФ, пределах.

! Мат на картинке/в комментарии. Ваш комментарий будет скрыт. При злоупотреблении возможен бан.

! Флуд - дублирующиеся комментарии от одного и того же пользователя в разных постах, систематические ложные вызовы модераторов с помощью функции @moderator, необоснованные обращения в техническую поддержку сайта, комментарии не несущие смысловой нагрузки и состоящие из хаотичного набора букв. Санкции - предупреждение с дальнейшим баном при рецидиве.

! Публикация рекламных постов. Несогласованное размещение рекламного материала, влечет незамедлительную приостановку действий учетной записи пользователя.

! Публикация материала, запрещенного на территории РФ и преследуемого УК РФ. Незамедлительная приостановка действия учетной записи пользователя.

! Мультиаккаунты. Использование нескольких активных аккаунтов, принадлежащих одному пользователю (исключение - дополнительный аккаунт для обращения в тех. поддержку при блокировке основного аккаунта) запрещено. За нарушение предусмотрено отключение основного аккаунта с возможной дальнейшей блокировкой любого аккаунта от данного пользователя.

Правила

! Мат на картинке/в комментарии. Ваш комментарий будет скрыт. При злоупотреблении возможен бан.

Лучший комментарий

desperados24

444

11 лет назад

я конечно могу ошибаться но большая часть фишкарей включая меня ни фига не понимают в подобных уравнениях И УЖ ТОЧНО ДУХ У НАС НЕ ЗАХВАТЫВАЕТ ОТ НЕГО .... ЛИЧНО МОЁ МНЕНИЕ.. ГЫГЫГЫ

-8

Удалить комментарий?

Удалить Отмена

Игорь

desperados24

31k

11 лет назад

К сожалению не ошибаешься. Так и есть - вы поколение ЕГЭ и даже вышку в ВУЗе будете сдавать тестами. Совершенно не понимая сути.

Удалить комментарий?

Удалить Отмена

Фельдъегерь

desperados24

11 лет назад

Это абсолютно не означает, что их не нужно пытаться понять или, хотя бы, иметь о них представление, так сказать, для общего развития

Удалить комментарий?

Удалить Отмена

desperados24

Игорь

444

11 лет назад

вы уважаемый прежде чем ляпать без разбора, что да как, абсолютно не зная человека! ради приличия просто что бы не выглядеть балаболом, как в данном случае!!! Начнем с начала(меня такие как вы мягко говоря цепляют): Высшее юрист, работаю по профессии, сразу после армии1 Экзамены в школе сдавал обычным, так сказать, дедовским способом! вышку получал в течении 5 лет тем же дедовским способом, Потому что я не из богатой семьи был!!!! Так вот прежде чем балаболить на подобные темы где попало,начни диалог с человеком, если уж так хочется умом коротким блеснуть! Судя по всему это вашему мега умному поколению спасибо сказать надо, за то что ЕГЭ вами упомянутое ввели! И за то что нынешние школьники не то что писать разговаривать не умеют! Я так понимаю из ваших слов сам примерно за сорок, так вот вспомните свои годы когда вас старшее поколение примерно теми же словам называли что и вы сейчас , так было и будет всегда! Может вы помните, когда военную "срочку" перевили с 3 лет службы на 2, что говорили о двухгодичниках 3-хгодичники???? ПОМНИТЕ, или может в курсе??? а сегодня блин 1 год служат суббота воскресенье выходные, спят в обед в обязалово ходят в берцах и носки носят!!! для меня это тоже бред!!! ну ни чего живём же!!! Так что попрошу вас воздержаться от подобных высказываний!!! сегодняшние школьники абсолютно не причем, что они сдают ЕГЭ и жёстко сидят на флеше с wi-fi... это не они подсели на него а старшее поколение не доглядело в лице правительства в лице учителей чиновников и конечно родителей!!! А ваши высказывания подобные под стать бакиным охам и ахам , какие мл засранцы!!))))))))0

Удалить комментарий?

Удалить Отмена

desperados24

Фельдъегерь

444

11 лет назад

И к вам ниже написанное относится судя по всему?

Удалить комментарий?

Удалить Отмена

Фельдъегерь

desperados24

11 лет назад

по чему всему?

Удалить комментарий?

Удалить Отмена

Игорь

desperados24

31k

11 лет назад

О людях судят по поступкам. Ваш поступок - обГЫГЫкать непонятные буквы, никак не тянет на поступок образованного человека, уважающего достижения великих ученых в остальных направлениях.
Вот и получайте тогда.
А если в следующий раз, когда уважаемый юрист (хм... а есть такие вообще?) здесь напишет формулу:
количество чиновников России - чиновники России которых надо посадить за коррупцию = 0
я вместо того, чтобы проникнуться глубиной мысли, напишу "первый нах" - буду так же справедливо закидан презрением.

Удалить комментарий?

Удалить Отмена

Frank Borman

7 лет назад

На самом деле, теорема Эйлера (или формула Эйлера) звучт так:

exp(iθ) = cosθ + isinθ

в частном случае, если θ = π, то получим:

exp(iπ) = cosπ + isinπ = -1 => exp(iπ) + 1 = 0

Удалить комментарий?

Удалить Отмена

боряконстантинов

11 лет назад

"... иррациональное число (с бесконечным количеством цифр) ..." - сомнительное определение.. 1/3, если расписать десятично, тоже имеет бесконечно много знаков

Удалить комментарий?

Удалить Отмена

Показать 68 комментариев