Брахистохрона
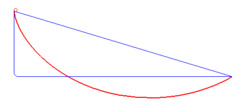
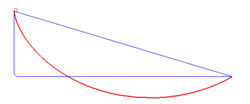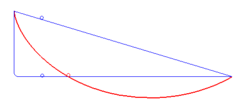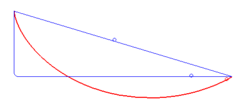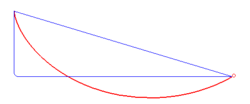
Брахистохро́на (от греч. βράχιστος — кратчайший и χρόνος — время) — кривая скорейшего спуска. Задача о её нахождении была поставлена в 1696 году Иоганном Бернулли (Википедия)
Источник:
На "Фишках" с разной периодичностью выкладывали эту гифку. Движение тел по различным траекториям. Красная линия — брахистохрона.
Источник:
Кому эта тема показалась интересной, велком на просмотр. В этом видео ведущий Майкл вместе с Адамом Сэвиджем строят стенд для проверки решения задачи о брахистохроне, а заодно проверяют теоретическое свойство таутохроны на практике.
Посты на ту же тему




45 комментариев
8 лет назад
Удалить комментарий?
Удалить Отмена8 лет назад
Удалить комментарий?
Удалить Отмена8 лет назад
Удалить комментарий?
Удалить Отмена8 лет назад
Удалить комментарий?
Удалить Отмена8 лет назад
Удалить комментарий?
Удалить Отмена8 лет назад
Удалить комментарий?
Удалить Отмена8 лет назад
Удалить комментарий?
Удалить Отмена8 лет назад
Можно даже привести пример. Если самолету надо переместиться на 500км по горизонтали, то летя прямо он, возможно, немного отстанет от самолета, который летит снижаясь. Но он пролетит намного быстрее самолета, который на протяжении всего пути набирает высоту.
Удалить комментарий?
Удалить Отмена8 лет назад
Удалить комментарий?
Удалить Отмена8 лет назад
А горизонтальная скорость это и есть то, что отвечает за разрыв в месте встречи.
Как следствие, в крутом пике увеличивается, в первую очередь, суммарная скорость и заметно вырастает путь. Выигрыш в горизонтальной скорости "съестся" энергозатратами на подъеме. На видео, обратите внимание, он начал с высоты более 5км а при наборе потерял всю скорость не долетев даже до 2км, при этом он все еще поднимался, т.е. его горизонтальная скорость, в этот момент, была ниже начальных 500км/ч.
Удалить комментарий?
Удалить Отмена8 лет назад
ПС, ты тот ролик то видал?
Удалить комментарий?
Удалить Отмена8 лет назад
Да и сам первый маневр это скорее парабола, а не циклоида. Вот второй пример, напротив, гораздо ближе к циклоиде. И там нету фазы подъема, которая съедает всю скорость.
Удалить комментарий?
Удалить Отмена8 лет назад
Удалить комментарий?
Удалить Отмена8 лет назад
Удалить комментарий?
Удалить Отмена