Эти столешницы одинаковой формы, но ваш мозг не позволит вам увидеть это
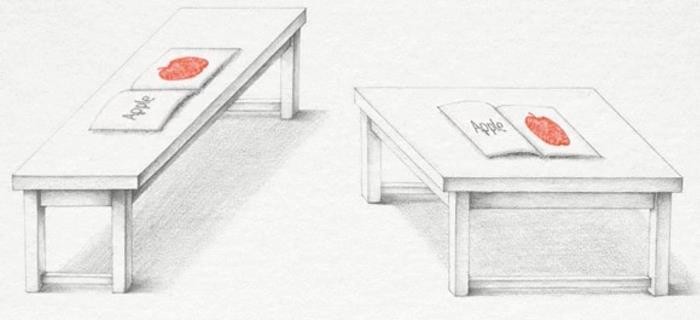
Эта иллюзия Шепарда показывает два стола, которые кажутся совершенно разными по размеру: один длинный и один почти квадратный.
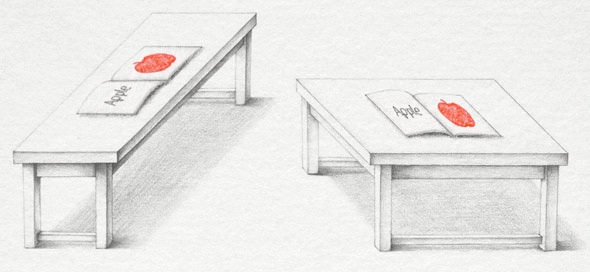
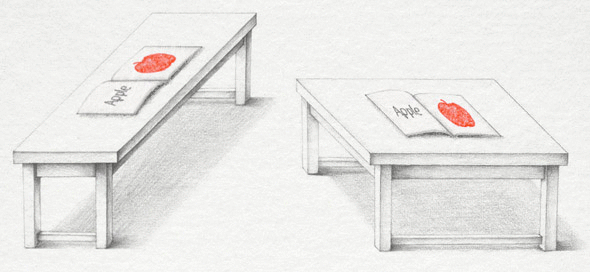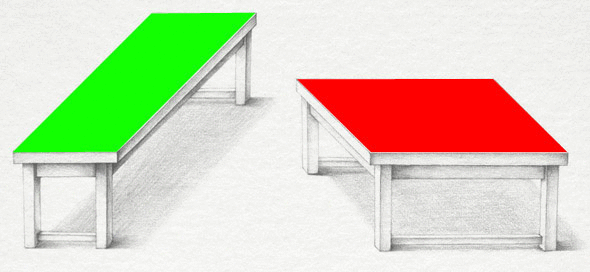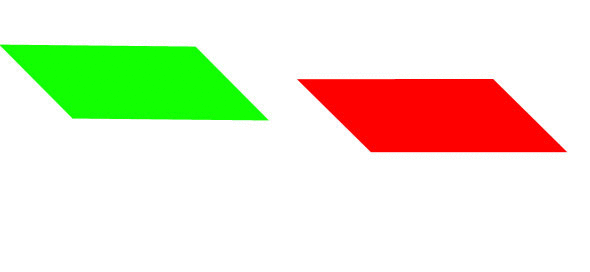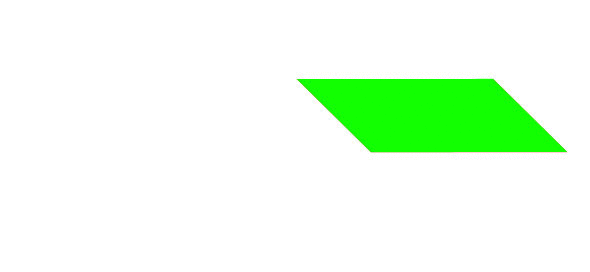
Но манипулируя формами, образованными столешницами, мы понимаем, что столешницы на самом деле абсолютно одинаковы.
Источник:
Суть в том, что, оказывается, наш мозг хочет воспринимать вещи в 3D:
«Если есть возможность интерпретировать рисунок или изображение как трехмерный объект, мы это делаем. Две столешницы имеют совершенно одинаковую двухмерную форму на странице, исключая угол поворота. Никто не верит в это, когда впервые смотрит на иллюзию. Иллюзия показывает, что мы не видим двухмерную форму, нарисованную на странице, но вместо этого мы видим трехмерный вид объекта в пространстве», — говорит Дэвид Хегер из Университета Нью-Йорка.
Таким образом, наш мозг, желающий видеть 3D, интерпретируют поверхность стола, уходящую в «перспективу», подобно физическому объекту, делающему то же самое в реальном мире — как вытянутую и более тонкую.
Источник:


177 комментариев
8 лет назад
Суть в том, Дорогой автАр, что нарисованные в 3D вещи наш мозг пытается воспринимать как 3D вещи. Ох! Уенно познавательный пост!
Удалить комментарий?
Удалить Отмена8 лет назад
з.ы. шпециально для афтара сего опуса: Докажем что 2+2=5 и 2 * 2 = 5, тоже равно 5. То есть 4=5 . Запишем сначала очевидное равенство 25 - 45 = 16 - 36 . Прибавим (9/2)^2 к обеим частям 25 - 45 + (9/2)^2 = 16 - 36 + (9/2)^2. Или 5^2 - (2 * 5 * 9)/2 + (9/2)^2 = 4^2 - (2 * 4 * 9)/2 + (9/2)^2. Отсюда(5-9/2)^2 = (4-9/2)^2. Обе части положительны, можно извлечь квадратный корень. 5 - 9/2 = 4 - 9/2. Теперь прибавим 9/2 к обеим частям уравнения: 5 = 4 что и требовалось доказать. Итак, 2*2 = 5 и 2+2=5.
Удалить комментарий?
Удалить Отмена