Доказательство того, что 2x2=5
В детстве мы все зубрили таблицу умножения. Похоже, что зря зубрили... Вот вам доказательство того, что 2x2=5
Что и требовалось доказать!
Источник:
Посты на ту же тему
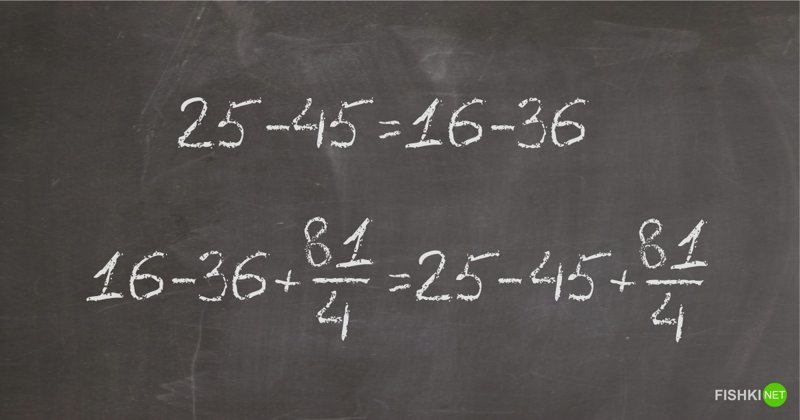
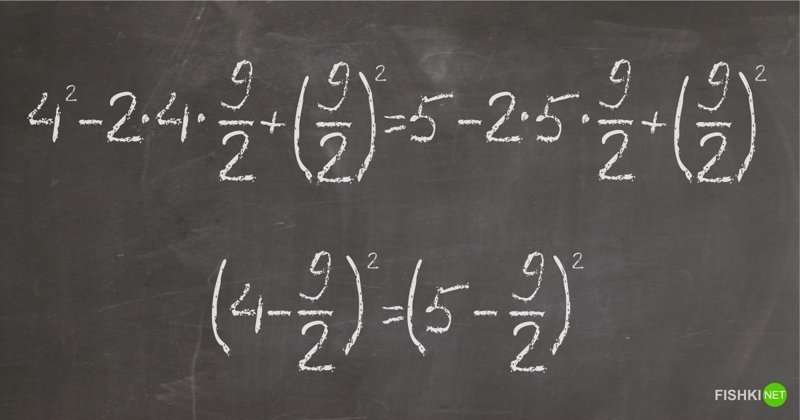
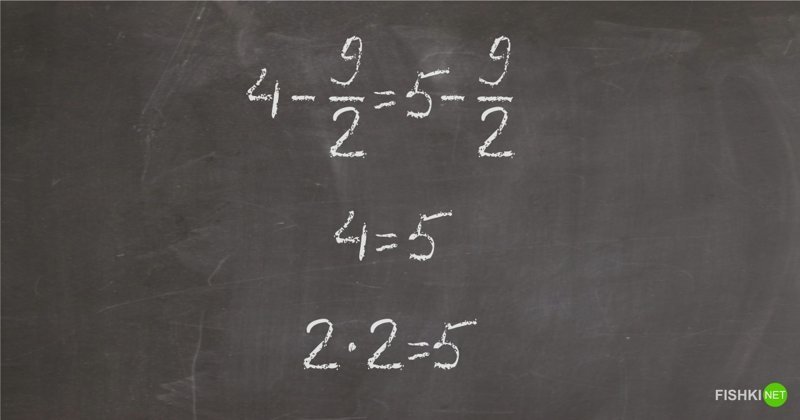


453 комментария
8 лет назад
Удалить комментарий?
Удалить Отмена8 лет назад
(4 - 9/2)^2 = (5 - 9/2)^2.
Однако всем кто знаком с арифметикой известно что для любого положительного числа существуют два числа возведение в квадрат которых даёт данное число, квадрат иногда и меня приводил к подобной ошибке (Хотя возможно автор нашёл, а может и сам придумал эту задачку просто что-бы кто-то лишний раз немного подумал)
Например:
a^2 = 4 => a = -2 или a = +2
То есть когда мы берём корень избавляясь от чётной степени то получаем два возможных случая.
Например
(x + 5)^2 = 16 => x + 5 = 4 или x + 5 = -4
Так и в данном случае:
(4 - 9/2)^2 = (5 - 9/2)^2 => 4 - 9/2 = +(5 - 9/2) или 4 - 9/2 = -(5 - 9/2)
В первом случае: 4 - 9/2 = +(5 - 9/2) => 4=5 (Не верно)
Во втором случае: 4 - 9/2 = -(5 - 9/2) => 4 - 4 - 1/2 = -5 + 4 + 1/2 =>
4 - 4 = -5 + 4 +1 => 0=0 (Верно!!!)
Вот и вся история.
Важно так-же запомнить, (Сколько раз я наступал на эти грабли учась в школе)
Уравнение f^2(x) = g^2(x) приводит к двум уравнениям, если имеет смысл избавиться от квадратов: f(x) = +g(x) и f(x) = -g(x). Решения этих двух уравнений являются и решениями исходного уравнения f^2(x) = g^2(x).
И наоборот решения уравнения f^2(x) = g^2(x) являются решениями и не менее одного уравнения полученного после избавления от квадратов
Если имеет смысл возвести в квадрат уравнение f(x) = g(x) и дальше решать уравнение
f^2(x) = g^2(x). То решениями уравнеия f^2(x) = g^2(x) будут и решения уравнения
f(x) = -g(x). И могут появиться лишние корни.
Вот наверное и всё что можно сказать по данному вопросу. Ну и поблагодарить автора за интересную задачку.
Удалить комментарий?
Удалить Отмена