Как полюбить математику?
Чем больше домашних работ делал с сыном, тем больше стал копаться, думать логически и пришел к выводу, что нелюбовь к математике обусловлена простым непониманием. В школе все зубрят, но понимать не понимают.
С детства мы просто заучиваем правила и теоремы и пытаемся их применить к той или иной задаче, но вероятнее, что математика больше про логическое решение задачи и нахождение разных путей решения, даже если своих)
Стал ловить себя на мысли, что расслабляюсь пока думаю над какой-нибудь задачкой.
Разминаю мозги и медитирую, так сказать.
Находил задачи, которые можно представить абстрактно или визуализировать.
Самые любимые детские:
Задача про отель с бесконечным числом номеров, в который приезжает хоккейная команда с бесконечным количеством игроков. Надо решить, как поселить команду, если все номера в отеле уже заняты. Эта задача, сформулированная в 1924 году немецким математиком Давидом Гильбертом, помогает объяснить понятие «бесконечность» и то, что с бесконечностью невозможно работать также, как с обычными числами.
Задачка про то, что математика это про интуицию и понимание происходящего. Не все задачи обязательно решаемы. Как и в жизни)
Дзен!
Задачка с ответом на риторический вопрос “Почему”?
Если ее визуализировать с помощью бумаги, перекрутив и потом разрезать, то она не распадется на две части, как цилиндр. А если резать по краям, то будут получаться новые ленты мёбиуса.
Любопытно почему?
Потому что лента имеет только одну сторону, а связанность (двухмерность) фигуры не позволяет ей распасться или получить новые фигуры)
Увлекательно же?
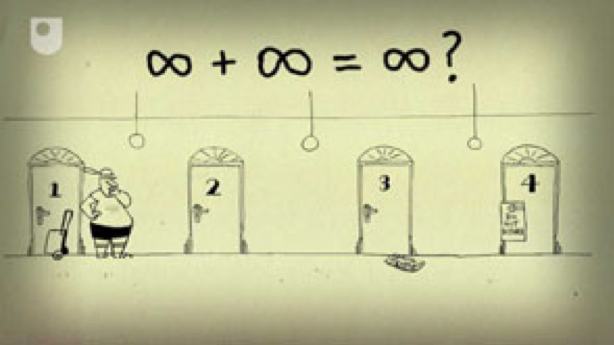



27 комментариев
6 лет назад
Удалить комментарий?
Удалить Отмена6 лет назад
Удалить комментарий?
Удалить ОтменаУдалить комментарий?
Удалить Отмена6 лет назад
Удалить комментарий?
Удалить Отмена6 лет назад
Удалить комментарий?
Удалить Отмена6 лет назад
Удалить комментарий?
Удалить Отмена6 лет назад
Удалить комментарий?
Удалить ОтменаУдалить комментарий?
Удалить Отмена