Как увидеть динозавров и мамонтов с помощью черной дыры и телескопа
Возможно ли увидеть настоящих живых динозавров или мамонтов? Конечно нет, скажет каждый. Но если хорошо подумать, то в принципе есть варианты :). На данном этапе развития технологий — это практически недостижимо, но теоретически возможно.
Итак, как же увидеть прошлое? Для этого нужно поймать свет от Земли, который был искривлен черной дырой на 180 градусов. Расстояние до черной дыры в световых годах должно быть равно половине количества лет, на которые требуется увидеть прошлое. Т.е. если хочется увидеть динозавров, 100 млн. лет назад, то расстояние до черной дыры должно быть 50 млн. световых лет. Тогда свет дойдет до черной дыры за 50 млн. лет и 50 млн. лет будет идти обратно до Земли. Суммарная задержка светового сигнала как раз составит 100 млн. лет.
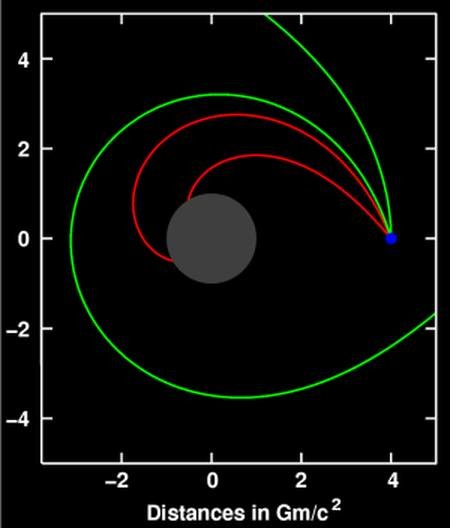
На этой картинке из Википедии показана одна из возможных траекторий света вблизи черной дыры (зеленые и красные линии, это возможные траектории светового луча вблизи черной дыры, показанной серым).
Источник:
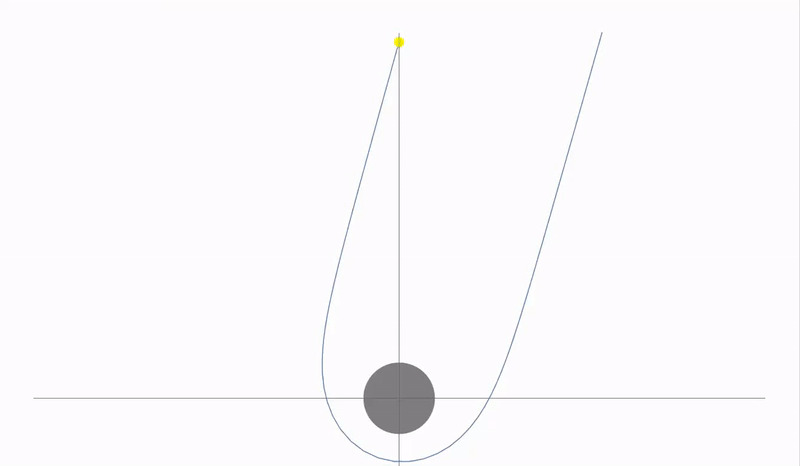
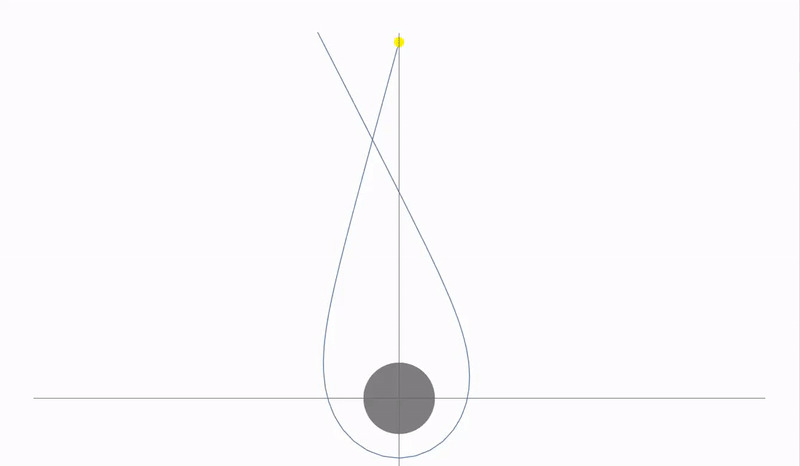
Или даже так, отклоняясь на 220 градусов
Источник:
Выглядит как интересная теория, а как дело обстоит на практике? Попробуем ответить на практические вопросы:
- Есть ли подходящие черные дыры?
- Какой нужен телескоп, чтобы увидеть динозавров с разрешением, например, 1 см?
Подходящие чёрные дыры
Если открыть статью Википедии "Кандидаты в чёрные дыры", то можно найти пару подходящих черных дыр. Одна в центре нашей Галактики (Расстояние 26000 световых лет) Стрелец А* и вторая в галактике М60, она же Messier 60 и NGC 4649 (60 млн. световых лет). Стрелец А* позволит нам увидеть мамонтов и неандертальцев — 52000 лет назад, а М60 динозавров — 120 млн. лет назад.
Какой же нужен телескоп
Подходящие черные дыры найдены, осталось рассчитать и построить телескоп, в который можно все это увидеть. У каждого телескопа есть предельная разрешающая способность, которая определяется диаметром объектива. Если выполнить точный расчет, какой должен быть диаметр объектива телескопа. чтобы можно было разглядеть мамонта с разрешением 10 см с расстояния 52000 световых лет, то получаем число 1.67*10e+12 км (1670000000000 км) или 1.67 триллиона километров. Для динозавров с расстоянием 120 млн. световых лет получается примерно в 2000 раз больше — 3.85*10e+15 км (3850000000000000 км) или 3.85 тыс. триллионов километров. Чтобы проще представить эти числа, сравним их с диаметром орбиты Нептуна. Для мамонтов нужен телескоп диаметром 186 орбит Нептуна, для динозавров 428000 орбит Нептуна. Выглядит многовато и абсолютно не реалистично. Но наука не стоит на месте, последние исследования в квантовой механике говорят о том, что возможно преодоление дифракционного предела для телескопа с помощью квантово запутанных (entangled) фотонов или квантового усиления света по аналогии с лазером. Вот несколько ссылок на статьи по этой теме:
http://physicsworld.com/cws/article/news/2014/apr/29/quantum-telescope-could-make-giant-mirrors-obsolete
https://medium.com/the-physics-arxiv-blog/how-to-build-a-quantum-telescope-5f473cf5a4bc#.px6glqnha
https://arxiv.org/pdf/1604.06928.pdf
Так что вполне возможно через 50-100 лет с помощью подобных технологий мы сможем увидеть настоящих динозавров. А прослушать радиопередачи, которые транслировались 50 лет назад, может быть получится и с помощью современных радиотелескопов. Но это уже отдельная история.
Другие технические трудности
Вероятно, при искривлении света черной дырой, изображение будет очень сильно искажено, как например на этой фотографии
где линия улыбки — это искажённое гравитацией изображение.
Может быть его удастся восстановить с помощью постобработки, а может быть и нет. Чтобы решить эту проблему, можно использовать не черную дыру, а обычные звезды, такие как наше Солнце. Например, Солнце отклоняет свет примерно на 1 угловую секунду. Чтобы отклонить свет на 180 градусов, потребуется 648 тысяч солнц. В нашей Галактике (Млечный Путь) содержится 200—400 млрд. звезд, что вполне достаточно для этой задачи :)
Источник:






65 комментариев
9 лет назад
Удалить комментарий?
Удалить ОтменаУдалить комментарий?
Удалить Отмена9 лет назад
Удалить комментарий?
Удалить Отмена