Эти крестьянские дети действительно это в уме считали?

В 1867 году уехал в родную деревню Татево Тверской губернии. Построил первую в России сельскую школу с общежитием для крестьянских детей. Сам стал директором и одновременно вел уроки математики.
Издавал «Татевский сборник» - альманах с произведениями Е. Баратынского, В. Жуковского, А. Фета, П. Вяземского. И сам писал талантливые статьи о литературе, живописи, музыке. Сотрудничал с жтурналом «Сельская школа» и сочинил два возможных сюжета для опер Чайковского . Сам написал для своей школы учебник по математике и другие методические пособия.
В школьной художественной мастерской Сергей Александрович занимался с детьми живописью, черчением и рисованием.
В 1891 году Академия наук избрала С.А.Рачинского своим Член-корреспондентом.
Константин Победоносцев, крупнейший политический деятель тех лет, писал о нём императору Александру III в 1883 году:
«Вы изволите припомнить, как несколько лет тому назад я докладывал Вам о Сергее Рачинском, почтенном человеке, который, оставив профессорство в Московском университете, уехал на житьё в своё имение, в самой отдалённой лесной глуши Бельского уезда Смоленской губернии, и живёт там безвыездно вот уже более 14 лет, работая с утра до ночи для пользы народной. Он вдохнул совсем новую жизнь в целое поколение крестьян… Стал поистине благодетелем местности, основав и ведёт, с помощью 4 священников, 5 народных школ, которые представляют теперь образец для всей земли. Это человек замечательный.
Всё, что у него есть, и все средства своего имения он отдаёт до копейки на это дело, ограничив свои потребности до последней степени»

Картину нарисовал его друг, художник Николай Богданов-Бельский.
И в ней поражает два момента.
Во-первых, сам Сергей Александрович . Представляете – народная школа, крестьянские дети – и учитель в костюме с бабочкой.
Учитель идет на урок и надевает бабочку. Тут ощущается какая-то прямо глубинная воспитанность, человечность, интеллигентность в самом лучшем смысле.
Во-вторых, пример на доске.

Что и говорить, пример и сейчас непростой для устного счета. Вот это и поражает – крестьянские дети и такое задание.
Сергей Александрович понемногу прививал любовь к математике, используя, в том числе и разные любопытные штучки.
Однажды он сам обнаружил, что есть вот такая интересная закономерность:

Именно вторая строка из его небольшого открытия задействована в этом примере.
То есть если знать об этом, то достаточно рассчитать и сложить квадраты чисел 10,11,12, и вторая часть примера на доске с числами 13,14 будет равна первой сумме.
Делов-то, да? «Удивительные дети».
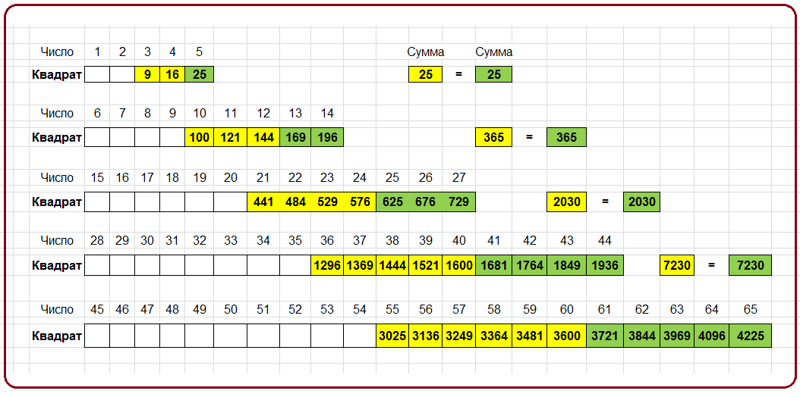
Потом уже и мне стало интересно – а ведь наверняка эта закономерность будет и дальше продолжаться. Так и получается, и структура закономерности хорошо видна на этой картинке.

Безусловно, можно эту закономерность формализовать в общем виде, но как-то не увидел в этом смысла.

Художник Федор Решетников. «Опять двойка»