Сейчас узнаем, кто из нас жертва ЕГЭ
Пробуем решить две детские арифметические задачки позапрошлого века!
На этой известной картине изображён реальный человек. Это профессор Московского университета Сергей Александрович Рачинский.
В 70-х годах XIX века Рачинский неожиданно бросил карьеру, жильё в Москве и приличное профессорское жалование – и уехал в село Татево в Тверской области, чтобы преподавать математику крестьянским детям.
Кстати, автор картины, художник Николай Богданов-Бельский, был одним из учеников Сергея Александровича. А какую же задачу они решают? Давайте присмотримся...
Попробуете сделать то же самое, что делали крестьянские дети в конце позапрошлого века – решить эту задачу «в уме»? Подумайте! А пока ещё одна задачка – от писателя Антона Павловича Чехова.
В его рассказ «Репетитор» семиклассник Зиберов занимается с Петей Удодовым, готовя его к поступлению во второй класс гимназии. Там есть весьма любопытная задача...
«Купец купил 138 аршин черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?»
Попробуем решить её так, как учит современный учебник алгебры. Пусть x – количество купленного синего сукна, а y – количество купленного чёрного сукна. Тогда составляем систему уравнений:
5x + 3y = 540
x + y = 138
Собственно, семиклассник Зиберов об этом догадывается:
– Эта задача, собственно говоря, алгебраическая, — говорит он. — Ее с иксом и игреком решить можно.
Однако вот что интересно! В рассказе папа будущего второклассника Пети, купец Удодов, решает эту головоломную задачу без алгебры!
– И без алгебры решить можно, — говорит Удодов, протягивая руку к счетам и вздыхая.
– Вот, извольте видеть...Он щелкает на счетах, и у него получается 75 и 63, что и нужно было.
– Вот-с... по-нашему, по-неученому.
Получается, что задача всё-таки арифметическая? Что её можно решить, обладая знаниями на уровне второго класса? Попробуйте догадаться, как купец Удодов решил задачу, не глядя в дальнейший текст...
Решение первой задачи
Итак, сначала разберём задачу профессора Рачинского. Решить эту задачу можно несколькими способами. Нам нравится красивое решение через арифметическую прогрессию: известно, что квадраты чисел 10, 11, 12, 13 и 14 отличаются друг от друга на числа, образующие прогрессию с разностью 2 – то есть 21, 23, 25 и 27. Поэтому
Ну а дальше делим 730 на 365 и получаем в ответе 2. Однако самое простое решение – через так называемые «последовательности Рачинского». Это красивое арифметическое открытие Сергей Александрович совершил самостоятельно и широко использовал для составления таких вот хитрых задач. Оказывается, что:
И так далее. В частности, сумма во второй строке равна 365. Тогда в задаче на картине на доске сверху в дроби, по сути, записано 365 + 365, а делим мы это всё на 365 – то есть в ответе получаем 2 буквально за считанные секунды!
Решение второй задачи
Предположим, что купец купил только синее сукно, все 138 аршин. Тогда он заплатил бы 138 х 5 = 690 рублей. А он заплатил только 540. Почему?
Потому что он купил не только дорогое синее сукно, но и более дешёвое чёрное. Разница в деньгах составляет 690 – 540 = 150 рублей.
А разница в цене между синим и чёрным сукном составляет 5 – 3 = 2 рубля. Делим 150 на 2 и получаем 75 аршин чёрного сукна.
Ну а оставшегося синего – совсем просто: 138 – 75 = 63.
Источник:







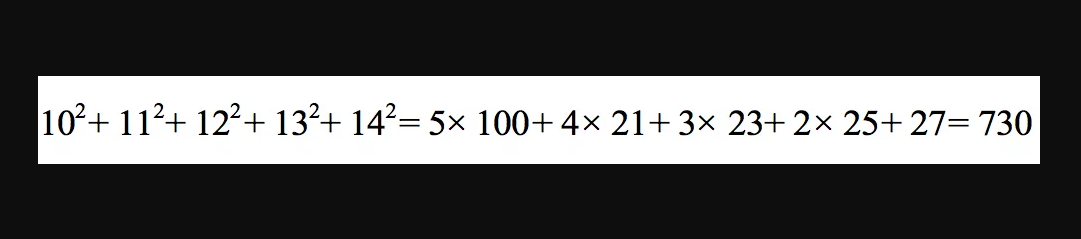
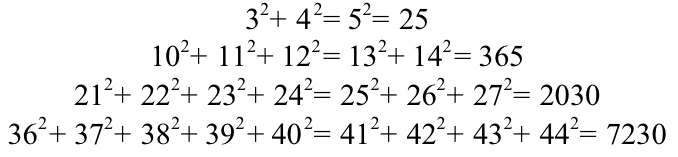


45 комментариев
3 года назад
Удалить комментарий?
Удалить Отмена3 года назад
Удалить комментарий?
Удалить Отмена3 года назад
Переформулируем.
(12-2)^2+(12-1)^2+12^2+(12+1)^2+(12+2)^2
Возьмем первую и последнюю скобки раскроем их и приведем подобные, в результате получим: 2*12^2+8.
Для второй и четвертой скобки аналогично: 2*12^2+2.
И для всего выражения: 5*12^2+10.
12^2=144.
144*5=144*10/2=720.
720+10=730.
730/365=2.
Источник:
Пробуем решить две детские арифметические задачки позапрошлого века!
Удалить комментарий?
Удалить Отмена