7 самых противоречивых парадоксов в математике
Самое Интересное предлагает вашему вниманию 7 самых противоречивых математических парадоксов.
Парадокс №1. Парадокс Монти Холла
Задача формулируется как описание игры, основанной на американском телешоу «Let’s Make a Deal», и названа в честь ведущего этой передачи. Наиболее распространённая формулировка этой задачи, опубликованная в 1990 году в журнале Parade Magazine, звучит следующим образом:
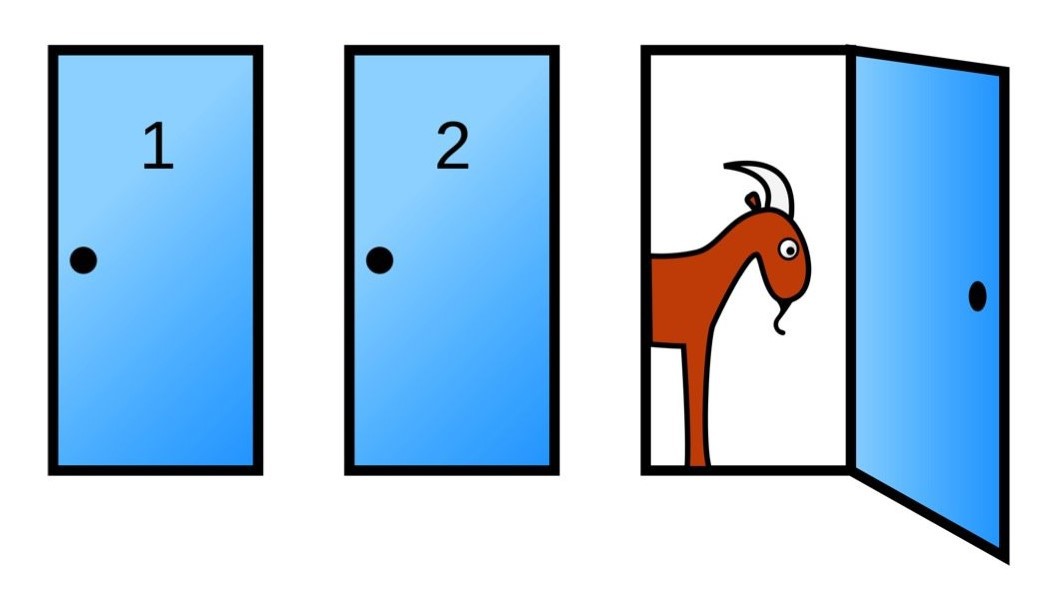
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, №1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, №3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь №2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Решить парадокс Монти Холла в свою пользу можно простым способом – всегда менять выбранную дверь! После открытия первой двери, за которой скрывалась одна из коз, становится ясно, что машина прячется за одной из оставшихся двух дверей (хотя мы и не знаем, за какой именно). Большинство участников шоу не видят преимущества в смене двери, полагая, что их шансы на победу остались все те же – 33.3%. Однако это не так! На самом деле, шансы на выигрыш автомобиля после изменения первоначального выбора возрастают в два раза. Да, первоначально шансы выиграть авто равняются 33.3% при любом выборе, однако после открытия одной из дверей с козой, шансы того, что автомобиль скрывается за оставшейся, третьей дверью, — 66.6%.
Легче всего подсчитать эти вероятности, если представить, что вы выбираете между «своей» дверью (вероятность 33.3%) и комбинированными вероятностями двух оставшихся дверей (66.6% соответственно). Ведь когда вы выбираете одну из дверей, вероятность того, что автомобиль за какой-то из двух других, равняется 66.6% — и когда за одной из этих дверей оказывается коза, вероятность для оставшейся остается 66.6%.
Парадокс №2. 0,9999…=1
0,(9) или 0,999 («ноль и девять в периоде») — периодическая десятичная дробь, представляющая число 1. Другими словами, 1=0{,}(9).
У этого равенства существует несколько доказательств, основанных на теории пределов.
Одно из них:
Парадокс №3. Парадокс дней рождения
Парадокс дней рождения — утверждение, что если дана группа из 23 или более человек, то вероятность того, что хотя бы у двух из них дни рождения (число и месяц) совпадут, превышает 50%. Для группы из 60 или более человек вероятность совпадения дней рождения хотя бы у двух её членов составляет более 99%, хотя 100% она достигает, только когда в группе не менее 366 человек (с учётом високосных лет — 367).
Такое утверждение может показаться противоречащим здравому смыслу, так как вероятность одному родиться в определённый день года довольно мала, а вероятность того, что двое родились в конкретный день — ещё меньше, но является верным в соответствии с теорией вероятностей. Таким образом, оно не является парадоксом в строгом научном смысле — логического противоречия в нём нет, а парадокс заключается лишь в различиях между интуитивным восприятием ситуации человеком и результатами математического расчёта.
Один из способов понять на интуитивном уровне, почему в группе из 23 человек вероятность совпадения дней рождения у двух человек столь высока, состоит в осознании следующего факта: поскольку рассматривается вероятность совпадения дней рождения у любых двух человек в группе, то эта вероятность определяется количеством пар людей, которые можно составить из 23 человек. Так как порядок людей в парах не имеет значения, то общее число таких пар равно числу сочетаний из 23 по 2, то есть 23 × 22/2 = 253 пары. Посмотрев на это число, легко понять, что при рассмотрении 253 пар людей вероятность совпадения дней рождения хотя бы у одной пары будет достаточно высокой.
Ключевым моментом здесь является то, что утверждение парадокса дней рождения говорит именно о совпадении дней рождения у каких-либо двух членов группы. Одно из распространённых заблуждений состоит в том, что этот случай путают с другим — похожим, на первый взгляд, — случаем, когда из группы выбирается один человек и оценивается вероятность того, что у кого-либо из других членов группы день рождения совпадёт с днем рождения выбранного человека. В последнем случае вероятность совпадения значительно ниже.
Парадокс №4. Задача трех узников
Трое заключённых, A, B и С заключены в одиночные камеры и приговорены к смертной казни. Губернатор случайным образом выбирает одного из них и милует его. Стражник, охраняющий заключённых, знает, кто помилован, но не имеет права сказать этого. Заключённый A просит стражника сказать ему имя того (другого) заключённого, кто точно будет казнён: «Если B помилован, скажи мне, что казнён будет C. Если помилован C, скажи мне, что казнён будет B. Если они оба будут казнены, а помилован я, подбрось монету, и скажи имя B или C».
Стражник говорит заключённому A, что заключённый B будет казнён.
Заключённый A рад это слышать, поскольку он считает, что теперь вероятность его выживания стала 1/2, а не 1/3, как была до этого. Заключённый A тайно говорит заключённому С, что B будет казнен. Заключённый С также рад это слышать, поскольку он всё ещё полагает, что вероятность выживания заключённого А — 1/3, а его вероятность выживания возросла до 2/3. Как такое может быть?
Неправильный ответ заключается в том, что заключённый A не получил информацию о своей собственной судьбе. Заключённый A до того, как спросить стражника, оценивает свои шансы как 1/3, так же как B и C. Когда стражник говорит, что B будет казнён, это всё равно, что вероятность того, что С помилован (вероятность 1/3) или A помилован (вероятность 1/3), и монета, выбиравшая между B и C, выбрала B. (Вероятность — 1/2; в целом вероятность того, что назван B — 1/6, поскольку A помилован). Поэтому, узнав, что B будет казнён, заключённый A оценивает шансы на помилование таким образом: его шансы теперь — 1/3, но теперь, зная, что B точно будет казнён, шансы С на помилование теперь 2/3.
Правильный ответ заключается в том, что после получения информации от стражника о казни В, шансы на помилования В равны нулю. Потому что только в двух случаях охранник мог произнести имя В — в случае помилования С и в случае, если подброшенная монетка выпала на В. Но какой из двух случаев определил указание охранником осуждённого В как такого, что будет казнён не известно. За условиями задачи, охранник не мог назвать имя заключённого А как такого, что будет казнён. Поэтому заключённый А ничего не узнал о собственной судьбе. Первоначальные условия его неизвестности не изменились. Изменились лишь условия для заключённых С и В. Первый еще имеет шанс на помилование, а второй уже точно будет казнён.
Парадокс №5. Закон Бенфорда
Закон Бенфорда или закон первой цифры гласит, что в таблицах чисел, основанных на данных источников из реальной жизни, цифра 1 на первом месте встречается гораздо чаще, чем все остальные. Более того, чем больше цифра, тем меньше вероятности, что она будет стоять в числе на первом месте.
Если же вы посмотрите на реальные цифры, то заметите, что «9″ встречается гораздо реже, чем в 11% случаев. Также куда меньше цифр, чем ожидалось, начинается с «8″, зато колоссальные 30% чисел начинаются с цифры «1″. Эта парадоксальная картина проявляется во всевозможных реальных случаях, от количества населения до цен на акции и длины рек.
Закон Бенфорда был открыт вовсе не Бенфордом, а американским астрономом Шимоном Ньюкомбом. Примерно в 1881 г. Ньюкомб заметил, что страницы тетради с логарифмическими таблицами, на которых числа начинались с 1, гораздо сильнее захватаны и истрепаны, чем страницы, на которых числа начинались с 2 и так далее до 9 – те выглядели чистыми, как будто их вообще не открывали. Ньюкомб предположил: те страницы, которые больше всего истрепались, чаще всего и открывали, и на основании своих наблюдений заключил: те ученые, которые до него брали тетрадь, работали с данными, отражавшими подобное распределение цифр. Закон же был назван по фамилии Франка Бенфорда, который в 1938 г. заметил то же самое, что и Ньюкомб, когда просматривал логарифмические таблицы в научно-исследовательской лаборатории «Дженерал Электрик» в г. Скенектади, штат Нью-Йорк. Он обнаружил, что частота появления цифры в качестве первой падает по мере того, как цифра увеличивается от одного до девяти. То есть «1″ появляется в качестве первой цифры примерно в 30,1% случаев, «2″ появляется около 17,6% случаев, «3″?—?примерно в 12,5%, и так далее до «9″, выступающей в качестве первой цифры всего лишь в 4,6% случаев.
Чтобы понять это, представьте себе, что вы последовательно нумеруете лотерейные билеты. Когда вы пронумеровали билеты от одного до девяти, шанс любой цифры стать первой составляет 11,1%. Когда вы добавляете билет № 10, шанс случайного числа начаться с «1″ возрастает до 18,2%. Вы добавляете билеты с № 11 по № 19, и шанс того, что номер билета начнётся с «1″, продолжает расти, достигая максимума в 58%. Теперь вы добавляете билет № 20 и продолжаете нумеровать билеты. Шанс того, что число начнётся с «2″, растёт, а вероятность того, что оно начнётся с «1″, медленно падает.
Парадокс №6. Почему ваши друзья, скорее всего, популярнее вас?
Парадокс дружбы был впервые вскрыт в 1991 году Скоттом Фелдом, работавшим социологом в State University of New York в Стоун Бруке. В то время, разумеется, доктор Фелд основывался на «настоящих» социальных связях, нежели на онлайн-сетях. Позднее, в прошлом году, учёные из Cornell University подтвердили действенность выводов и для активных пользователей Facebook* (721 млн людей на момент исследования, связанных 69 млрд узами виртуальной дружбы). В действительности же результат справедлив для любой сети, где несколько её членов более популярны, нежели иные. Проистекает же это из простой арифметики.
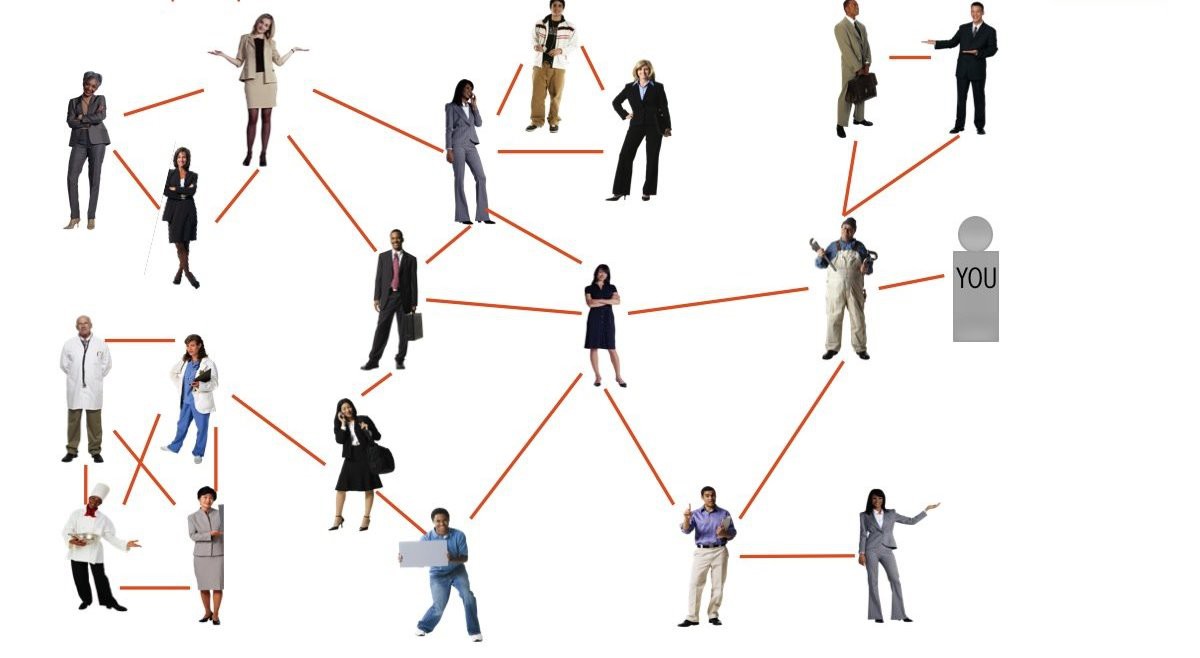
Давайте рассмотрим этот парадокс на примере офиса, состоящего из 20 человек. Красными линиями обозначены друзья:
Среднее количество друзей у каждого человека равно 3,39.
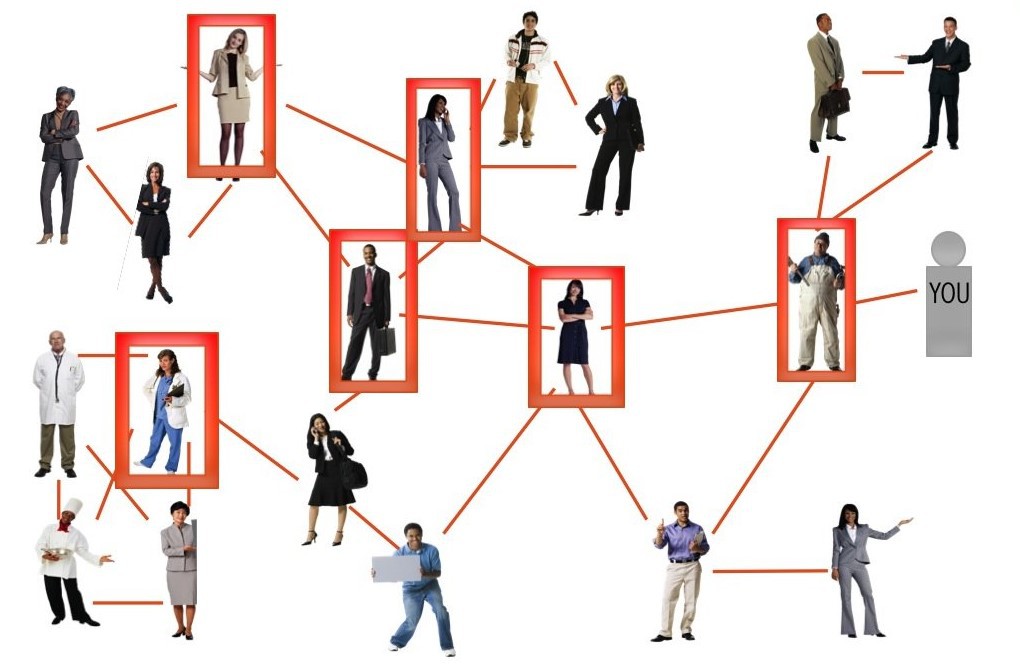
В красные квадраты заключены сотрудники, у кого друзей больше среднего. Они самые популярные в коллективе. Что еще более примечательно, 17 сотрудников из 20 дружат хотя бы с одним из них:
Парадокс №7. Любой неправильный четырехугольник формирует параллелограм
Четырехугольник может быть любой формы. Главное условие — 4 угла и прямые стороны.
* Запрещены в РФ








52 комментария
9 лет назад
Удалить комментарий?
Удалить Отмена9 лет назад
Удалить комментарий?
Удалить Отмена9 лет назад
"На пальцах": было 100 вариантов событий. Ситуация 1.
После открытия 98 дверей из 100 - стало 2 варианта. Ситуация 2. Осталось всего 2 варианта событий.
Она отличается от ситуации 1 тем, что была "выборка"...
"Совсем на пальцах": открытие 98 "пустых" дверей - это перевод одной статистической выборки в другую. Как ни прыгай, но осталось всего 2 варианта выбора ( 1 положительный, 1 отрицательный, остальные "отрицательные результаты" уже "спринтом" были сделаны). Из варианта 1:99 произошел переход 1:2 поскольку было 98 выборок "отрицательных". Апостериорная вероятность, т.е. вероятность наступления статистически редкого события после множества наступлений статистически частых. Она растет.
"Ну абсолютно на пальцах": игра "орел-решка".
При каждом броске вероятность выпадения одинакова. НО! Если была серия бросков, в которых выпала "решка", то вероятность выпадения "орла" - 1/2 БЕЗ учета предыстории. А с учетом ее - увеличивается. Поскольку ПО СТАТИСТИКЕ - количество выпадений "орла" и "решки" должны быть равны, причем чем больше бросков - тем меньше разница. Соответственно по статистике - чем больше выпало "орлов" - тем больше вероятность выпадения "решки" (чтобы статистика оказалось верной), с учетом именно предыдущей выборки.
Ну совсем-совсем-совсем на пальцах...
Чем больше длина выборки, тем меньше вероятность события "выпал подряд только орел", по сравнению с "много раз орел, а потом - решка". ("По-умному" - "закон больших чисел", т.е. чем больше выборка, тем больше вероятность ВСЕХ статистических вариантов).
А процветание казино обеспечивает лунка "Зеро", которая приводит к изменению пропорций. Если бы не "Зеро", то игра (по терминологии теории игр) была бы справедливой. "Черное-красное" и т.п. - 18/36 (1/2) выигрыш-проигрыш равны. А вот "Зеро" - это уже 18/37 выигрыш, 19/37 проигрыш для игрока, вот эти 3% разницы (18/37 и 19/37) и составляют доход казино (с учетом "большого" выигрыша на Зеро, который тем не менее меньше справедливого - казино же владельца должно кормить :) ).
Так что у меня для тебя ОЧЕНЬ плохая новость - формулы, может и помнишь, но что они обозначают - не понимаешь.
Удалить комментарий?
Удалить Отмена9 лет назад
На схеме ниже описана ситуация.
есть 3 варианта:
машина за 1ой ,2ой или 3ей дверью
если выбриаем 1ую дверь(и остаемся при своём выборе то выигрываем только в 1ом случае в 2ом и 3ем проигрываем)
если решаем поменять дверь, то в 1ом проигрываем во 2ом и 3ем выигрываем. Т.е. если меняем свое решения то в 2ух ситациях из 3ех мы в выигрыше.
Удалить комментарий?
Удалить Отмена9 лет назад
Иногда, мне кажется, что лучше вообще не пытаться доказывать что-то кому-то, кто не в состоянии просто критически мыслить.
Удалить комментарий?
Удалить Отмена9 лет назад
Удалить комментарий?
Удалить Отмена9 лет назад
Удалить комментарий?
Удалить Отмена